関連するページを見るにはこのグラフ図を利用してください．

極限 x →0　sinx /x

${\displaystyle \underset{x\to 0}{lim}\frac{sinx}{x}=1}$

■解説動画

◇関連動画一覧のページへ

■導出

I． $x>0$  の場合

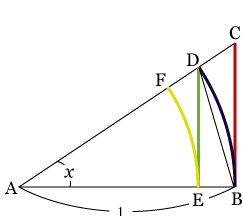
右のような図形を考える． ${\displaystyle \text{AB}=1}$ ， ${\displaystyle \angle \text{BAC}=x}$ （弧度法），弧 ${\displaystyle \text{BA}}$ は半径１の，弧 ${\displaystyle \text{EF}}$ は半径 ${\displaystyle cosx}$ である．このとき，

${\displaystyle sinx}$ ＝ ${\displaystyle \text{DE}}$ ， ${\displaystyle x}$ ＝弧 ${\displaystyle \text{BD}}$

よって，図形を用いて説明すると

となる．直感的に，この値は１より小さい値であるとわかる．

予備知識として，弧 ${\displaystyle \text{EF}}$ （ ${\displaystyle xcosx}$ ）， ${\displaystyle \text{DE}}$ （ ${\displaystyle sinx}$ ），弧 ${\displaystyle \text{BD}}$ （ ${\displaystyle x}$ ）， ${\displaystyle \text{BC}}$ （ ${\displaystyle tanx}$ ）の長さの関係を導いておくことにする．

扇形 ${\displaystyle \text{AEF}}$ の面積＝ ${\displaystyle \frac{1}{2}x{\left(cosx\right)}^2}$ ，三角形 ${\displaystyle \text{AED}}$ ＝ ${\displaystyle \frac{1}{2}cosxsinx}$ ，三角形 ${\displaystyle \text{ABD}}$ ＝ ${\displaystyle \frac{1}{2}sinx}$

扇形 ${\displaystyle \text{ABD}}$ の面積＝ ${\displaystyle \frac{1}{2}x}$ ，三角形 ${\displaystyle \text{ABC}}$ の面積＝ ${\displaystyle \frac{1}{2}tanx}$

扇形 ${\displaystyle \text{AEF}}$ の面積＜三角形 ${\displaystyle \text{AED}}$ の面積 より

三角形 ${\displaystyle \text{AEA}}$ の面積＜扇形 ${\displaystyle \text{ABD}}$ の面積＜三角形 ${\displaystyle \text{ABC}}$ の面積 より

(1)，(2)より

$x\cos x<\sin x<x<\tan x$ ･･････(3)

表現を変えると

弧 ${\displaystyle \text{EF}}$ （ ${\displaystyle xcosx}$ ）の長さ＜ ${\displaystyle \text{DE}}$ （ ${\displaystyle sinx}$ ）の長さ＜弧 ${\displaystyle \text{BD}}$ （ ${\displaystyle x}$ ）＜ ${\displaystyle \text{BC}}$ （ ${\displaystyle tanx}$ ）の長さ　･･････(4)

となる．

${\displaystyle \frac{sinx}{x}}$ を求めるとき，はさみうちの手法を用いることにする．(3)の左から3辺分の関係と ${\displaystyle x>0}$ より

となる．したがって， ${\displaystyle x\to 0}$  ならば， ${\displaystyle cosx\to 1}$  となり

${\displaystyle \underset{x\to 0}{lim}\frac{sinx}{x}=1}$

が導かれる．また，(3)の右から3辺分の関係と $\sin x>0$ より

となり同様にして

${\displaystyle \underset{x\to 0}{lim}\frac{sinx}{x}=1}$ ･･････(7)

が導かれる．

II． $x<0$  の場合

$x<0$ とし， $x=-t$ とおく． $t>0$ ，かつ， $x\to 0$  のとき $t\to 0$  である．よって

${\displaystyle \underset{x\to 0}{\lim }\frac{\sin x}{x}=\underset{t\to 0}{\lim }\frac{\sin \left(-t\right)}{-t}}$ ${\displaystyle =\underset{t\to 0}{\lim }\frac{-\sin t}{-t}}$ ${\displaystyle =\underset{t\to 0}{\lim }\frac{\sin t}{t}=1}$

となる

I，IIより

$x>0$ ， $x<0$  のいずれの場合も

${\displaystyle \underset{x\to 0}{\lim }\frac{\sin x}{x}=1}$

が成り立つ．

 

ホーム>>カテゴリー別分類>>その他>>極限の公式>>極限 x→0　sinx/x

最終更新日 2025年2月21日

[ページトップ]

利用規約

google translate (English version)