|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
写像の合成
2つの写像 ,がある. 集合 の要素 は写像 により,集合 の要素に対応し,集合 の要素 は,写像 により,集合Zの要素に対応する. と の写像を続けて行うことにより,集合 の要素 は集合 の要素に対応する.このように2つの写像を連続して行う対応を写像の合成といい,合成された写像(合成写像)を とすると,
で表す.
合成写像の概念を図で示すと下図のようになる.
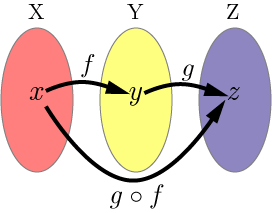
集合の要素 の像は .集合 の要素の像は となる.これを式で表すと,
・・・・・・(1)
・・・・・・(2)
となる.2つの式を合成すると((1)を(2)に代入すると),
となる.合成写像 による集合 の要素の像は と表される.
最終更新日 2023年4月13日