関連するページを見るにはこのグラフ図を利用してください．

逆写像

写像 ${\displaystyle f:\text{X}\to \text{Y}}$  が1対1の写像であるとき，${\displaystyle X}$ の要素x に対応する${\displaystyle Y}$ の要素をy とすると，この対応関係において${\displaystyle X}$ の写像f の値域${\displaystyle Z}$ に含まれる${\displaystyle Y}$ の要素y に対応する${\displaystyle X}$ の要素はx ただ1つ定まる．したがって，この${\displaystyle Y}$ の要素y から${\displaystyle X}$ の要素x への対応は写像と考えることができる．この写像をf の逆写像といい，

${\displaystyle f^{-1}}$  

で表す． 

逆写像の概念を図で示すと下図のようになる．

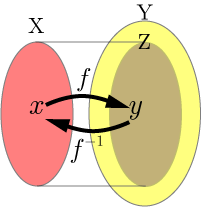
写像 f のつぎに逆写像${\displaystyle f^{-1}}$  を行う合成写像 $f^{-1}\circ f$  によって，Xの要素x の像は，自分自身になる．式で示すと，

${\displaystyle f^{-1}\left(f\left(x\right)\right)=x}$  

となる．

 

ホーム>>カテゴリー別分類>>その他>>写像>>逆写像

最終更新日 2022年7月15日

[ページトップ]

利用規約

google translate (English version)