関連するページを見るにはこのグラフ図を利用してください．

${\displaystyle tan\theta \geqq c}$ の求め方

単位円を用いて ${\displaystyle tan\theta \geqq c}$  を満たす$\theta$の範囲を求める． ただし， $\theta$の範囲は${\displaystyle \frac{\pi }{2}<\theta <\frac{3\pi }{2}}$とする．

単位円上の点の座標を用いた定義では

となる（ここを参照）．

1. まず，単位円を描き，${\displaystyle x=1}$と${\displaystyle x=-1}$ の2本の補助線を引く．座標${\displaystyle \left(1,c\right)}$ を点${\displaystyle \text{P}}$ とし，点${\displaystyle \text{P}}$ の原点に関して対称な点を点$\text{Q}$ とする．直線${\displaystyle \text{PQ}}$ と単位円との2つの交点（点${\text{P}}^{\prime }$，点${\text{Q}}^{\prime }$ ）の座標は

   ${\displaystyle y}$ 座標	${\displaystyle =c=\tan \theta }$
   ${\displaystyle x}$ 座標

   の関係を満たす（ここを参照）．
2. 次に，点${\displaystyle \text{P}}$ ，点${\displaystyle \text{Q}}$ からx 軸に下ろした垂線の足をそれぞれ点${\displaystyle \text{R}}$ ，点${\displaystyle \text{S}}$ とする．
   線分${\displaystyle \text{OP}}$ ，線分${\displaystyle \text{OQ}}$ とx軸とのなす角を${\displaystyle {\theta }_1}$ ，${\displaystyle {\theta }_2}$とする．
   直角三角形${\displaystyle \text{OPR}}$ の内角${\displaystyle \angle \text{POR}}$ ，${\displaystyle \text{OQS}}$ の内角${\displaystyle \angle \text{QOS}}$ を求め，${\displaystyle {\theta }_1}$ ，${\displaystyle {\theta }_2}$ を算出する．（三角形${\displaystyle \angle \text{OPR}}$ は${\displaystyle \text{OR}=1}$ ，${\displaystyle \text{RP}=c}$ の直角三角形 ）
3. 更に，θの範囲を単位円上に記入する．(左下図の場合は赤線で示してある）．

以上より，$\theta$の範囲（赤線部分）と${\displaystyle {\theta }_1\leqq \theta <\frac{1}{2}\pi }$ ，${\displaystyle {\theta }_2\leqq \theta <\frac{3}{2}\pi }$ （太い半透明の青線の部分）が重なった範囲${\displaystyle {\theta }_2\leqq \theta <\frac{3\pi }{2}}$ が解となる．

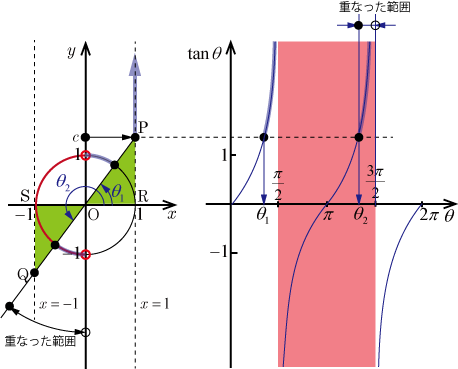
参考として，下図には単位円と ${\displaystyle tan\theta }$ のグラフとの関係を示しめす．

 

　ホーム>>カテゴリー分類>>三角関数>>三角不等式の解き方>>tanθ≧c の求め方

最終更新日： 2025年2月12日

[ページトップ]

利用規約

google translate (English version)