関連するページを見るにはこのグラフ図を利用してください．

三角関数計算の基礎

■関係式

■sinとcosのグラフの関係

　sinとcosの関係式を理解するのに役に立つグラフである．

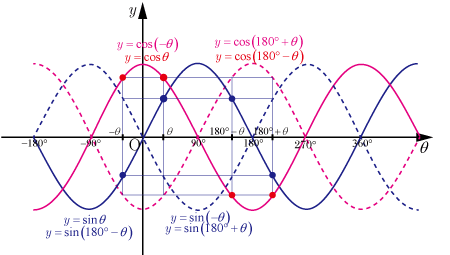
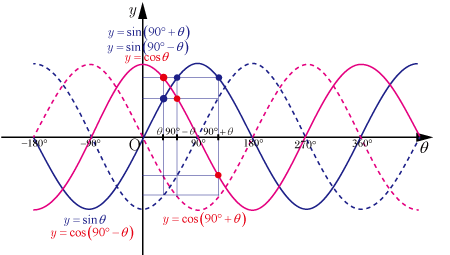
■導出

1.三角関数の定義より，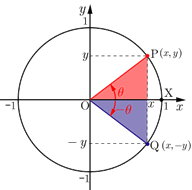

${\displaystyle \{\begin{array}{l}sin\theta =y\\ cos\theta =x\\ tan\theta =\frac{y}{x}\end{array}}$   ， ${\displaystyle \{\begin{array}{l}sin\left(-\theta \right)=-y\\ cos\left(-\theta \right)=x\\ tan\left(-\theta \right)=\frac{-y}{x}\end{array}}$

よって， 

$sin\left(-\theta \right)=-sin\left(\theta \right)$，$cos\left(-\theta \right)=cos\left(\theta \right)$,${\displaystyle tan\left(-\theta \right)=-tan\theta }$

2.三角関数の定義より，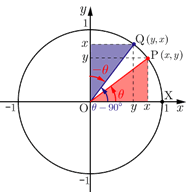

${\displaystyle \{\begin{array}{l}sin\theta =y\\ cos\theta =x\\ tan\theta =\frac{y}{x}\end{array}}$   ， ${\displaystyle \{\begin{array}{l}sin\left(90°-\theta \right)=x\\ cos\left(90°-\theta \right)=y\\ tan\left(90°-\theta \right)=\frac{x}{y}\end{array}}$

よって， 

$sin\left(90°-\theta \right)=cos\theta$，$cos\left(90°-\theta \right)=sin\theta$，${\displaystyle tan\left(90°-\theta \right)=\frac{1}{tan\theta }}$

3.三角関数の定義より，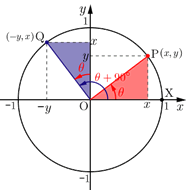

${\displaystyle \{\begin{array}{l}sin\theta =y\\ cos\theta =x\\ tan\theta =\frac{y}{x}\end{array}}$   ， ${\displaystyle \{\begin{array}{l}sin\left(90°+\theta \right)=x\\ cos\left(90°+\theta \right)=-y\\ tan\left(90°+\theta \right)=\frac{x}{-y}\end{array}}$

よって， 

$sin\left(90°+\theta \right)=cos\theta$，$cos\left(90°+\theta \right)=-sin\theta$，${\displaystyle tan\left(90°+\theta \right)=-\frac{1}{tan\theta }}$

4.三角関数の定義より，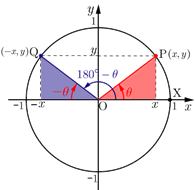

${\displaystyle \{\begin{array}{l}sin\theta =y\\ cos\theta =x\\ tan\theta =\frac{y}{x}\end{array}}$   ， ${\displaystyle \{\begin{array}{l}sin\left(180°-\theta \right)=y\\ cos\left(180°-\theta \right)=-x\\ tan\left(180°-\theta \right)=\frac{y}{-x}\end{array}}$

よって， 

$sin\left(180°-\theta \right)=sin\theta$， $cos\left(180°-\theta \right)=-cos\theta$，${\displaystyle tan\left(180°-\theta \right)=-tan\theta }$

5.三角関数の定義より，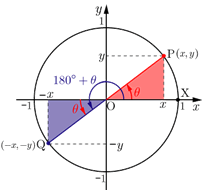

${\displaystyle \{\begin{array}{l}sin\theta =y\\ cos\theta =x\\ tan\theta =\frac{y}{x}\end{array}}$   ， ${\displaystyle \{\begin{array}{l}sin\left(180°+\theta \right)=-y\\ cos\left(180°+\theta \right)=-x\\ tan\left(180°+\theta \right)=\frac{-y}{-x}\end{array}}$

よって， 

$sin\left(180°+\theta \right)=-sin\theta$，$cos\left(180°+\theta \right)=-cos\theta$，${\displaystyle tan\left(180°+\theta \right)=tan\theta }$

 

ホーム>>カテゴリー分類>>三角関数>>三角関数計算の基礎

最終更新日：2023年3月9日

[ページトップ]

利用規約

google translate (English version)