tanθと単位円と直線x=1の関係
原点
と単位円上の点
を通る直線と
の直線の交点
の
座標の値
が
の値になる.
■証明
●
の場合
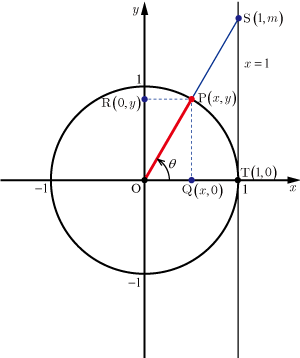
図1
の場合
の定義より
(∵△
∽
)
(∵
)
●
の場合
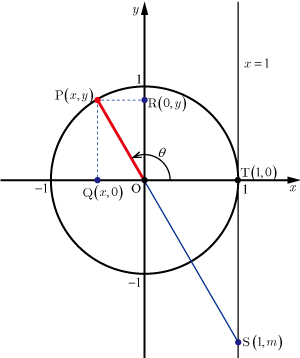
図2
の場合
の定義より
(∵
より
)
(∵△
∽
)
(∵
)
(∵
より
)
●
の場合
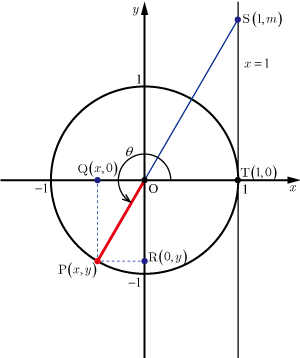
図3
の場合
の定義より
∵
より
,
より
(∵△
∽
)
(∵
)
●
の場合
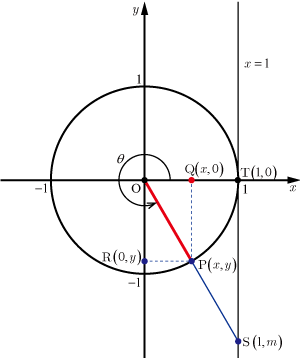
図4
の場合
の定義より
(∵
より
)
(∵△
∽
)
(∵
)
(∵
より
)
ホーム>>カテゴリー分類>>三角関数>>tanθと単位円と直線x=1の関係
最終更新日:
2025年2月12日