関連するページを見るにはこのグラフ図を利用してください．

1・サイン・コサイン三角形（注意：KIT数学ナビゲーション独特の呼び方）

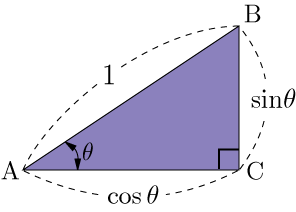三角関数を学習する基礎として，斜辺の長さが1である直角三角形を考える．

　三角比の定義より，

${\displaystyle \text{sin}\theta =\frac{\text{BC}}{\text{AB}}}$，${\displaystyle \text{cos}\theta =\frac{\text{AC}}{\text{AB}}}$

また，

${\displaystyle \text{AB}=1}$  

である．よって，

${\displaystyle \text{BC}=\text{sin}\theta }$  ， ${\displaystyle \text{AC}=\text{cos}\theta }$

となる．

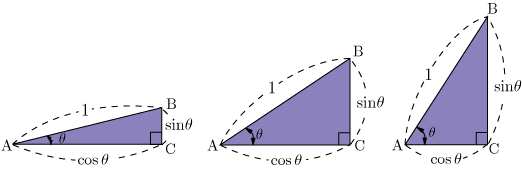
すなわち，斜辺の長さを1とすると辺の比が1：sinθ：cosθ となる．θ の値が変化してもこの比を表す式は変わらない．

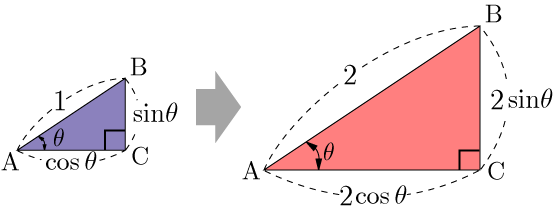
この三角形の辺の比を用いる．例えば，斜辺ABの長さが2になれば，辺BCの長さは2sinθ，辺ACの長さは2cosθとなる．

斜辺ABの長さが ${\displaystyle c}$ であれば，辺BCの長さは${\displaystyle csin\theta }$ ，辺ACの長さは${\displaystyle ccos\theta }$ となる．

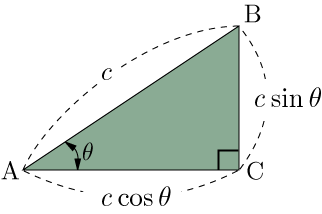
更にこの1・サイン・コサイン三角形を用いると簡単に，三角関数の相互関係が理解できる．

 

ホーム>>カテゴリー分類>>三角関数>>1・サイン・コサイン三角形

最終更新日： 2018年4月1日

[ページトップ]

利用規約

google translate (English version)