外積の大きさ

$\vec{a}$ と $\vec{b}$ のなす角を $θ$ とすると外積のベクトルの大きさ $| \vec{a} \times \vec{b} |$ は

$| \vec{a} | | \vec{b} | \sin θ$

となり， $\vec{a}$ と $\vec{b}$ を2辺とする平行四辺形の面積に相当する．

■証明

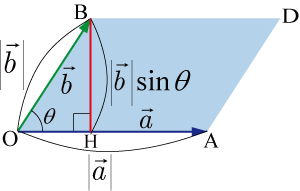平行四辺形OADBの底辺OAの長さは $| \vec{a} |$ ，
高さBHは三角形OBHの三角比より $| \vec{b} | \sin θ$ となる．

よって，平行四辺形の面積 $S$ は，

$S$ ＝底辺×高さ＝ $| \vec{a} | | \vec{b} | \sin θ$

となる．

$\vec{a} = (a_{x}, a_{y}, a_{z})$ ， $\vec{b} = (b_{x}, b_{y}, b_{z})$ とすると

$\vec{a} \times \vec{b}$ $= (a_{y} b_{z} - a_{z} b_{y}, a_{z} b_{x} - a_{x} b_{z}, a_{x} b_{y} - a_{y} b_{x})$

である（ここを参照）．

$|\vec{a}| |\vec{b}| \sin θ = |\vec{a}| |\vec{b}| \sqrt{1 - \cos^{2} θ}$

$\cos θ = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$ より

$= |\vec{a}| |\vec{b}| \sqrt{1 - {(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|})}^{2}}$

$= \sqrt{{(|\vec{a}| |\vec{b}|)}^{2} - {(\vec{a} \cdot \vec{b})}^{2}}$

${(|\vec{a}| |\vec{b}|)}^{2} - {(\vec{a} \cdot \vec{b})}^{2}$ を $\vec{a}$ ， $\vec{b}$ の成分で表すことにする.

${(|\vec{a}| |\vec{b}|)}^{2} - {(\vec{a} \cdot \vec{b})}^{2}$ $= (a_{x}^{2} + a_{y}^{2} + a_{z}^{2}) (b_{x}^{2} + b_{y}^{2} + b_{z}^{2})$ $- (a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z})$

$= a_{x}^{2} b_{x}^{2} + a_{x}^{2} b_{y}^{2} + a_{x}^{2} b_{z}^{2} + a_{y}^{2} b_{x}^{2} + a_{y}^{2} b_{y}^{2} + a_{y}^{2} b_{z}^{2} + a_{z}^{2} b_{x}^{2} + a_{z}^{2} b_{y}^{2} + a_{z}^{2} b_{z}^{2}$

$- \{{(a_{x} b_{x})}^{2} + {(a_{y} b_{y})}^{2} + {(a_{z} b_{z})}^{2} + 2 (a_{x} b_{x}) (a_{y} b_{y}) + 2 (a_{y} b_{y}) (a_{z} b_{z}) + 2 (a_{z} b_{z}) (a_{x} b_{x})\}$

$= a_{x}^{2} b_{y}^{2} - 2 (a_{x} b_{x}) (a_{y} b_{y}) + a_{y}^{2} b_{x}^{2}$ $+ a_{x}^{2} b_{z}^{2}$ $- 2 (a_{z} b_{z}) (a_{x} b_{x})$ $+ a_{z}^{2} b_{x}^{2}$ $+ a_{y}^{2} b_{z}^{2}$ $- 2 (a_{y} b_{y}) (a_{z} b_{z})$ $+ a_{z}^{2} b_{y}^{2}$

$= {(a_{x} b_{y} - a_{y} b_{x})}^{2} + {(a_{x} b_{z} - a_{z} b_{x})}^{2}$ $+ {(a_{y} b_{z} - a_{z} b_{y})}^{2}$

$= {(a_{y} b_{z} - a_{z} b_{y})}^{2} + {(a_{z} b_{x} - a_{x} b_{z})}^{2}$ $+ {(a_{x} b_{y} - a_{y} b_{x})}^{2}$

よって

$|\vec{a}| |\vec{b}| \sin θ$ $= \sqrt{{(a_{y} b_{z} - a_{z} b_{y})}^{2} + {(a_{z} b_{x} - a_{x} b_{z})}^{2} + {(a_{x} b_{y} - a_{y} b_{x})}^{2}}$

となる．すなわち， $\vec{a} \times \vec{b}$ の大きさは $\vec{a}$ と $\vec{b}$ を2辺とする平行四辺形の面積の値になっている．

ホーム>>カテゴリー分類>>ベクトル>>外積の大きさ

最終更新日 2022年6月26日