ベクトルの成分表示

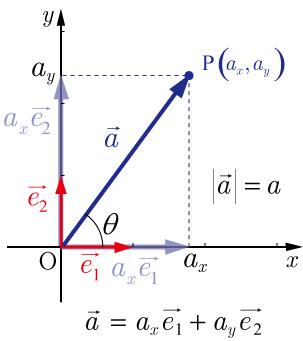
図1

${\displaystyle \overrightarrow{a}=a_x\overrightarrow{e_1}+a_y\overrightarrow{e_2}}$  

と基本ベクトル表示で表されたベクトルを

${\displaystyle \overrightarrow{a}=\left(a_x,a_y\right)}$  

のように表すことをベクトルの成分表示という．

ベクトルの大きさ ${\displaystyle \left|\overrightarrow{a}\right|=a}$ と， ${\displaystyle x}$ と ${\displaystyle \overrightarrow{a}}$ のなす角 ${\displaystyle \theta }$ を用いると

${\displaystyle a_x=a\cos \theta }$ ， ${\displaystyle a_y=a\sin \theta }$

となり 

${\displaystyle \overrightarrow{a}=\left(a\cos \theta ,a\sin \theta \right)}$  

となる． 

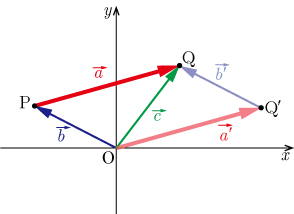
図2

■図2の ${\displaystyle \overrightarrow{a}}$ の成分表示

${\displaystyle \overrightarrow{a}}$ の始点が原点と重なるように を平行移動したものを， ${\displaystyle \overrightarrow{a^{\prime }}}$ とすると

${\displaystyle \overrightarrow{a^{\prime }}=\overrightarrow{a}}$ （ベクトルの相等）　･･････(1)

である．点${\displaystyle {\text{Q}}^{\prime }}$ の座標を${\displaystyle \left({q^{\prime }}_x,{q^{\prime }}_y\right)}$ とすると

${\displaystyle \overrightarrow{a^{\prime }}=\left({q^{\prime }}_x,{q^{\prime }}_y\right)}$

となる．一方

${\displaystyle \overrightarrow{a^{\prime }}=\overrightarrow{c}+\left(-\overrightarrow{b^{\prime }}\right)}$ ${\displaystyle =\overrightarrow{c}-\overrightarrow{b^{\prime }}}$ 　（逆ベゥトル，ベクトルの和）　･･････(2)

${\displaystyle \overrightarrow{b^{\prime }}=\overrightarrow{b}}$ 　（ベクトルの相等）　･･････(3)

(2)，(3)より

${\displaystyle \overrightarrow{a^{\prime }}=\overrightarrow{c}-\overrightarrow{b}}$　･･････(4)

(1)，(4)より

${\displaystyle \overrightarrow{a}=\overrightarrow{c}-\overrightarrow{b}}$

となる．点$\text{P}$の座標を${\displaystyle \left(p_x,p_y\right)}$，点$\text{Q}$の座標を${\displaystyle \left(q_x,q_y\right)}$とすると

${\displaystyle \overrightarrow{b}=\left(p_x,p_y\right)}$ ，${\displaystyle \overrightarrow{c}=\left(q_x,q_y\right)}$

より

${\displaystyle \overrightarrow{a}=\left(q_x,q_y\right)-\left(p_x,p_y\right)}$${\displaystyle =\left(q_x-p_x,q_y-p_y\right)}$

となる．

ホーム>>カテゴリー分類>>ベクトル>>ベクトルの成分表示

最終更新日：2025年10月7日