演習問題
■三角関数のグラフに関する問題, のグラフを描け ⇒ 解答
■三角関数のグラフに関する問題
次の三角関数のグラフを描け.
⇒ 解答
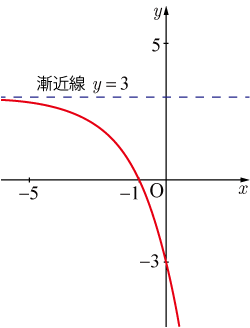
■基本的な指数関数のグラフ■基本的な指数関数のグラフ
■基本的な指数関数のグラフ
■基本的な指数関数のグラフ
■基本的な指数方程式の問題
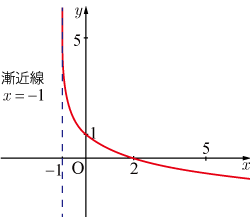
■基本的な対数関数のグラフ
■基本的な対数関数のグラフ
■基本的な対数関数のグラフ
■基本的な対数関数のグラフ
■基本的な指数方程式の問題
■定義域、値域、変化量に関する問題
■直線の方程式に関する問題
■直線の方程式に関する問題
■2次関数のグラフの平行移動に関する問題
■2次関数の 頂点 グラフ 最小値
■2次関数のグラフの平行移動に関する問題
■2次関数のグラフの平行移動に関する問題
■2次関数のグラフの拡大,平行移動に関する問題
■2次関数のグラフの拡大,平行移動に関する問題
■関数のグラフの拡大,平行移動に関する問題
■関数のグラフの拡大,平行移動に関する問題
■拡大⇒平行移動に関する問題
■2次曲線に関する問題
■逆関数に関する問題