問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

媒介変数表示における導関数

■問題

媒介変数(パラメータ)表示された関数 ${\displaystyle x=\sqrt{t-1}-2}$ ， ${\displaystyle y=t^3-5}$ について導関数 ${\displaystyle \frac{dy}{dx}}$ を $t$ の式で表し，点 ${\displaystyle \text{P}\left(-1,3\right)}$ における接線方程式を求めよ．

■解説動画

◇微分の動画一覧のページへ

■答

${\displaystyle \frac{dy}{dx}=6t^2\sqrt{t-1}}$

接線の方程式： ${\displaystyle y=24x+27}$

■解説

媒介変数表示における導関数り

${\displaystyle \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}}$ ･･････(1)

の式を用いる．

${\displaystyle \frac{dx}{dt}=\frac{1}{2}{\left(t-1\right)}^{-\frac{1}{2}}}$ ${\displaystyle =\frac{1}{2\sqrt{t-1}}}$ ･･････(2)

${\displaystyle \frac{dy}{dt}=3t^2}$ ･･････(3)

${\displaystyle f\prime (x)=0}$ とすると， ${\displaystyle x=\frac{2}{3},2}$

(1)に(2)，(3)を代入する．

${\displaystyle \frac{dy}{dx}=\frac{3t^2}{\frac{1}{2\sqrt{t-1}}}}$ ${\displaystyle =6t^2\sqrt{t-1}}$ ･･････(4)

点 ${\displaystyle \text{P}\left(-1,3\right)}$ における接線方程式を求める．

点 ${\displaystyle \text{P}\left(-1,3\right)}$ に対応する $t$ の値は， ${\displaystyle x=\sqrt{t-1}-2}$ の式に ${\displaystyle x=1}$ を代入して

${\displaystyle -1=\sqrt{t-1}-2}$

${\displaystyle \sqrt{t-1}=1}$

${\displaystyle t-1=1}$

${\displaystyle t=2}$ ･･････(5)

が求まる．(4)に(5)を代入する．

${\displaystyle \frac{dy}{dx}}$ ${\displaystyle =6\cdot 2^2\sqrt{2-1}}$ ${\displaystyle =24}$

よって，接線の方程式は

${\displaystyle y-3=24\left(x+1\right)}$

${\displaystyle y=24x+27}$ ･･････(6)

となる．

備考

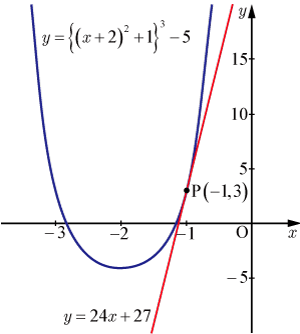
${\displaystyle y=f\left(x\right)}$ の形の式を求めてみる.

${\displaystyle x=\sqrt{t-1}-2}$ ･･････(7)

${\displaystyle y=t^3-5}$ ･･････(8)

(7)，(8)より， $t$ を消去する．

(7)より

${\displaystyle x+2=\sqrt{t-1}}$

${\displaystyle {\left(x+2\right)}^2=t-1}$

${\displaystyle t={\left(x+2\right)}^2+1}$ ･･････(9)

が得られる．(9)を(8)に代入すると関数の式が求まる．

${\displaystyle y={\left\{{\left(x+2\right)}^2+1\right\}}^3-5}$ ･･････(10)

　

ホーム>>カテゴリー分類>>微分>>微分に関する演習問題>>微分の計算問題>>媒介変数表示における導関数

最終更新日： 2025年2月21日

[ページトップ]

利用規約

google translate (English version)