|
|||||||||||||
|
|||||||||||||
|
問題を解くのに必要な知識を確認するにはこの知識グラフを利用してください.
基本的な1次変換の問題
■問題
座標平面において,直線 に関して対称な変換を表す表現行列を求めよ.
■答
■ヒント
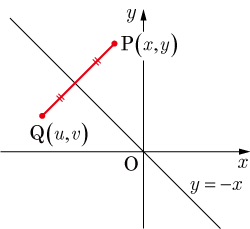
のグラフを描き,それに関して互いに対称な2点をとる.
線分の中点が直線上にあることと,線分と 直線 が直交することから,連立方程式を立てる.
とを,で表すことにより表現行列を求める.
■解き方
点,点の中点
が直線上にあることより
……(1)
点,点を通る直線の傾きは
となる.線分と 直線 が直交することとより
……(2)
より
……(3)
より
……(4)
より
よって
より
よって
したがって
よって,表現行列は
ホーム>>カテゴリー分類>>行列>>線形代数>>線形代数に関する問題>>線形写像・1次変換>>基本的な1次変換の問題
作成:学生スタッフ
最終更新日: 2023年2月10日