問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

直線の方程式に関する問題

■問題

点 ${\displaystyle \left(2,3\right)}$ を通り，傾きが ${\displaystyle \frac{1}{2}}$ である直線の方程式を求め，グラフをかけ．

■答

${\displaystyle y=\frac{1}{2}x+2}$

■ヒント

直線の方程式のページを参考にする．

■解説

点 ${\displaystyle \left(x_0,y_0\right)}$ を通り，直線の傾きが $a$ である直線の方程式は

${\displaystyle y-y_0=a\left(x-x_0\right)}$　･･････(1)

（直線の方程式のページの(5)の式）

である．

この問題の場合， ${\displaystyle \left(x_0,y_0\right)=\left(2,3\right)}$ ， 傾きは ${\displaystyle \frac{1}{2}}$ である.

よって，求める直線の方程式は

${\displaystyle y-3=\frac{1}{2}\left(x-2\right)}$

${\displaystyle y=\frac{1}{2}x-1+3}$

${\displaystyle y=\frac{1}{2}x+2}$

となる．

●別解1

(1)の式を覚えていなくても平行移動の考え方を適用するとよい．

求める直線の方程式のグラフは，原点を通り傾きが ${\displaystyle \frac{1}{2}}$ の直線

${\displaystyle y=\frac{1}{2}x}$　･･････(2)

のグラフを $x$ 軸方向に $2$ ， $y$ 軸方向に $3$ 平行移動したものになる，よって，求める直線の方程式は，(2)の $x$ を $x-2$ ， $y$ を $y-3$ に置き換えた

${\displaystyle y-3=\frac{1}{2}\left(x-2\right)}$

となる．これを整理すると

${\displaystyle y=\frac{1}{2}x+2}$

となる．

●別解2

直線の方程式は

$y=ax+b$　 （ $a$ ：直線の傾き, $b$ ： $y$ 切片） 　･･････(3)

（直線の方程式のページの(6)の式，1次関数のページも参照）

となることを知っていれば簡単に直線の方程式を導くことができる．この問題の場合は ${\displaystyle a=\frac{1}{2}}$ であるので，(3)は

${\displaystyle y=\frac{1}{2}x+b}$　･･････(4)

となる．直線が点 ${\displaystyle \left(2,3\right)}$ を通ることより， $x$ に $2$ ， $y$ に $3$ を代入しても(4)の関係は成り立つ．

よって

${\displaystyle 3=\frac{1}{2}\cdot 2+b}$

より

${\displaystyle b=2}$

が得られ，求める直線の方程式は

${\displaystyle y=\frac{1}{2}x+2}$

となる．

●直線のグラフ

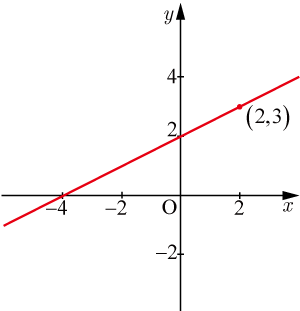
直線のグラフでは $x$ 切片と $y$ 切片が重要である． $y$ 切片は $2$ であることが分かっているので， $x$ 切片を求める．直線の方程式の $y$ に $0$ を代入すると

${\displaystyle 0=\frac{1}{2}x+2}$

${\displaystyle \frac{1}{2}x=-2}$

${\displaystyle x=-2\cdot 2=-4}$

となり， $x$ 切片は $-4$ である．よって，2点 ${\displaystyle \left(-4,0\right)}$ と ${\displaystyle \left(0,2\right)}$ を通る直線になる．

確かに，直線は点 ${\displaystyle \left(2,3\right)}$ を通っている．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>1次関数，2次関数などに関する問題>>直線の方程式に関する問題

最終更新日： 2024年9月26日

[ページトップ]

利用規約

google translate (English version)