問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

加法定理の問題の別解

■問題

${\displaystyle \text{sin18}°}$ の値を求めよ．

■答

${\displaystyle sin18°=\frac{-1+\sqrt{5}}{4}}$

■ヒント

底角が${\displaystyle 72°}$ の二等辺三角形に図のような補助線を引いて，${\displaystyle 18°}$ の角を作る．

 

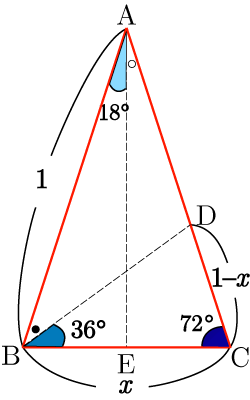
■解き方

${\displaystyle \text{AB}=1}$，${\displaystyle \text{BC}=x}$

とおく．

${\displaystyle \angle \text{ABC}}$ に二等分線を引き， ${\displaystyle \text{AC}}$ と交わる点を${\displaystyle \text{D}}$ とする．

${\displaystyle △\text{BCD}}$， ${\displaystyle △\text{ABD}}$が二等辺三角形より， (二等辺三角形である理由)

${\displaystyle \text{BD}=x}$，${\displaystyle \text{AD}=x}$

また，${\displaystyle \text{AB}=\text{AC}=1}$ より

${\displaystyle \text{DC}=1-x}$

となる．

${\displaystyle \angle \text{BAC}}$に二等分線を引き， ${\displaystyle \text{BC}}$と交わる点を${\displaystyle \text{E}}$とする．

以上をまとめた図が下の三角形である．

　　 

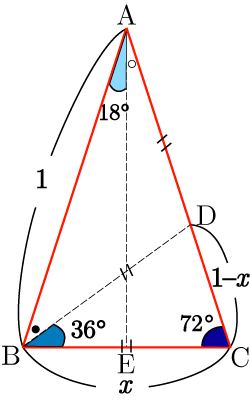
2角が等しいことより

${\displaystyle △\text{ABC}\backsim △\text{BCD}}$

である．よって

${\displaystyle \frac{\text{BC}}{\text{AB}}=\frac{\mathrm{CD}}{\text{BC}}}$

${\displaystyle \frac{x}{1}=\frac{1-x}{x}}$

${\displaystyle x^2=1-x}$

${\displaystyle x^2+x-1=0}$…(1)

${\displaystyle x>0}$より(1) の解は，解の公式を用いると

${\displaystyle x=\frac{-1+\sqrt{5}}{2}}$

となる．

${\displaystyle sin18°=\frac{\text{BE}}{\text{AB}}}$

${\displaystyle \text{BE}=\frac{1}{2}\text{BC}}$${\displaystyle =\frac{1}{2}\cdot \frac{-1+5}{2}}$${\displaystyle =\frac{-1+\sqrt{5}}{4}}$

したがって

${\displaystyle sin18°=\frac{\frac{-1+\sqrt{5}}{4}}{1}}$${\displaystyle =\frac{-1+\sqrt{5}}{4}}$

 

■${\displaystyle △\text{BCD}}$と ${\displaystyle △\text{ABD}}$が二等辺三角形の理由

${\displaystyle \text{BD}}$は${\displaystyle \angle \text{ABC}}$の二等分線であるので，${\displaystyle \angle \text{CBD}}$ は${\displaystyle \text{36}°}$

${\displaystyle \angle \text{BDC}=180°-72°-36°}$${\displaystyle =72°}$

したがって

${\displaystyle \angle \text{BCD}=\angle \text{BDC}}$

となり${\displaystyle △\text{BCD}}$は二等辺三角形である．

　

${\displaystyle \text{BD}}$は${\displaystyle \angle \text{ABC}}$の二等分線であるので，${\displaystyle \angle \text{ABD}}$は${\displaystyle \text{36}°}$．したがって

${\displaystyle \angle \text{ABD}=\angle \text{BAD}}$

となり${\displaystyle △\text{ABD}}$ は 二等辺三角形である．

 

 

 

ホーム>>カテゴリー分類>>三角関数>>問題演習>>加法定理に関する問題>>加法定理の問題

最終更新日： 2023年4月15日

[ページトップ]

利用規約

google translate (English version)