|
|||||||||||||
|
|||||||||||||
|
問題を解くのに必要な知識を確認するにはこの知識グラフを利用してください.
加法定理・合成関数に関する問題
■問題
次式を の形に変形しなさい.
■解説動画
◆三角関数の動画一覧のページへ
■答
■ヒント
(1)合成した時の係数 を求める.
(2)合成関数の公式を使い解を導きだす.
■解き方
より
・・・・・・(1)
と式を変形する.
・・・・・・(2)
の形に変形できる.(2)に加法定理を適用すると
・・・・・・(3)
となる.
(1)と(3)を比較すると
となる連立方程式が得られる.これを解くと(図参照)
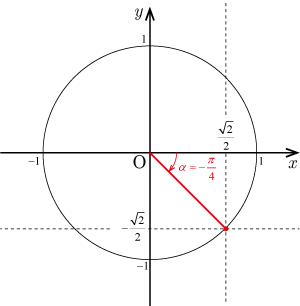
となる.したがって
となる.
●作図より求める方法
座標平面上に, の係数 を 成分, の係数 を 成分とする点 と原点 を結ぶ線分 を描く.線分 の長さが , 線分 と 軸となす角が角度 となる.
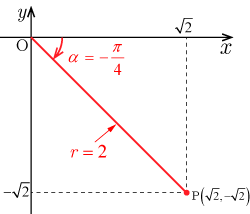
よって
,
となる.
ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>三角関数の合成>>加法定理・合成関数に関する問題
最終更新日: 2025年3月12日