問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

三角関数の方程式に関する問題

■問 題

次の方程式を解け．ただし， ${\displaystyle 0\leqq \theta <2\pi }$ とする．

${\displaystyle sin\theta =-\frac{1}{2}}$

■答

${\displaystyle \theta =\frac{7}{6}\pi ,\frac{11}{6}\pi }$

■ヒント

$\sin \theta =c$ の解き方

■解説

${\displaystyle sin\theta }$ の値は単位円上の点の ${\displaystyle y}$ 座標に相当する．( ここ を参照)

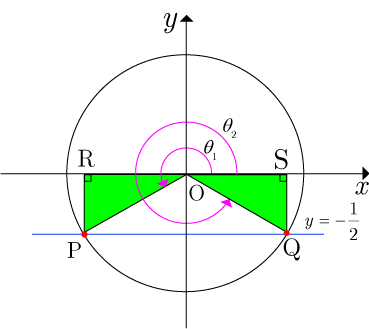
まず，図のように単位円 を描く．このとき，原点を ${\displaystyle \text{O}}$ とする．

${\displaystyle x}$ 軸と平行な線である ${\displaystyle y=-\frac{1}{2}}$ を描く．

描いた線と 単位円 との交点を ${\displaystyle \text{P}}$ ， ${\displaystyle \text{Q}}$ とし，原点 ${\displaystyle \text{O}}$ と線で結ぶ．

${\displaystyle \text{P}}$ ， ${\displaystyle \text{Q}}$ から ${\displaystyle x}$ 軸に垂線を引き，それぞれの足を ${\displaystyle \text{R}}$ ， ${\displaystyle \text{S}}$ とし，直角三角形 ${\displaystyle \text{OPR}}$ ， ${\displaystyle \text{OQS}}$ の内角を求める．

${\displaystyle \text{OP}=1}$ ， ${\displaystyle \text{PR}=\frac{1}{2}}$ より，基本的な三角形と照らし合わせると

${\displaystyle \angle \text{POR}=\frac{1}{6}\pi }$

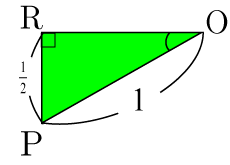
となる．よって

${\displaystyle {\theta }_1=\frac{1}{2}\pi +\frac{1}{6}\pi =\frac{7}{6}\pi }$

同様に ${\displaystyle {\theta }_2}$ を算出すると

${\displaystyle {\theta }_2=2\pi -\frac{1}{6}\pi =\frac{11}{6}\pi }$

となる．

　

ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>三角関数の方程式>>三角関数の方程式に関する問題

最終更新日： 2025年2月12日

[ページトップ]

利用規約

google translate (English version)