問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

三角関数の方程式に関する問題

■問題

次の方程式を解け．ただし， ${\displaystyle 0\leqq \theta <\pi }$とする．

${\displaystyle \tan \theta =\sqrt{3}}$

■答

${\displaystyle \theta =\frac{1}{3}\pi }$

■解説

${\displaystyle \tan \theta }$の値は，単位円において

に相当する(ここを参照)．

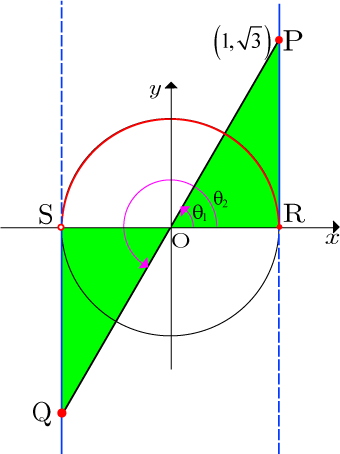
しかし，${\displaystyle \text{tan}\theta }$ を求める場合，底辺の長さが1である直角三角形を描くと高さが${\displaystyle \text{tan}\theta }$ になるので都合がよい．よって，以下のような作図をする．

まず，単位円を描く

${\displaystyle x=1}$ ，${\displaystyle x=-1}$ の直線を引く．

${\displaystyle \tan \theta =\sqrt{3}}$より，${\displaystyle x=1}$ 上の${\displaystyle y}$ の値が${\displaystyle \sqrt{3}}$ となるところを点${\displaystyle \text{P}}$とする．

点${\displaystyle \text{P}}$ と原点${\displaystyle \text{O}}$ を通る直線を描き，${\displaystyle x=-1}$ との交点を点${\displaystyle \text{Q}}$ とする．

点${\displaystyle \text{P}}$，点${\displaystyle \text{Q}}$ から ${\displaystyle x}$ 軸に垂線を下ろし，それぞれの足を${\displaystyle \text{R}}$ ，${\displaystyle \text{S}}$ とする．

直角三角形${\displaystyle \text{OPR}}$と直角三角形${\displaystyle \text{OQS}}$を描く．

この作図により，

${\displaystyle \text{tan}\left(\angle \text{POR}\right)=\tan {\theta }_1=\sqrt{3}}$

${\displaystyle \text{tan}{\theta }_2=\tan \left({\theta }_1+\pi \right)=\tan {\theta }_1=\sqrt{3}}$　(ここを参照)

となる．

${\displaystyle \text{OR}=1}$，${\displaystyle \text{PR}=\sqrt{3}}$より，基本的な三角形と照らし合わせると

${\displaystyle \angle \text{POR}={\theta }_1=\frac{1}{3}\pi }$

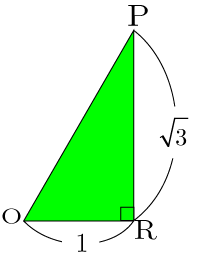
となる．

${\displaystyle \angle \text{QOS}=\frac{1}{3}\pi }$ より

${\displaystyle {\theta }_2=\pi +\frac{1}{3}\pi =\frac{4}{3}\pi }$

となる．

${\displaystyle 0\leqq \theta <\pi }$であるから(円周上の赤線に対応)，${\displaystyle {\theta }_2}$は範囲外となる．

よって，求める角は

${\displaystyle \theta =\frac{1}{3}\pi }$

となる．

　

ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>三角関数の問題>>三角関数の方程式に関する問題

学生スタッフ作成
最終更新日： 2024年3月5日

[ページトップ]

利用規約

google translate (English version)