|
|||||||||||||
|
|||||||||||||
|
問題を解くのに必要な知識を確認するにはこの知識グラフを利用してください.
三角関数不等式の問題
■問題
次の不等式を解け.ただし, とする.
■解説動画
◇三角関数の動画一覧のページへ
■答
,
■解説
まず, の範囲で
,
を満たす を求める.
以下の問題を参考にする.
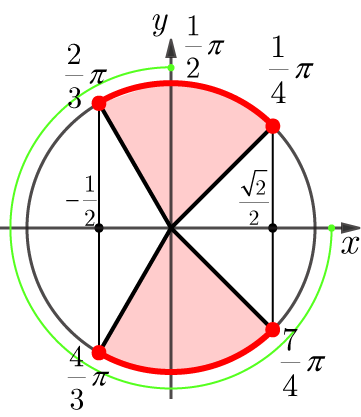 は単位円上の点の
成分に相当することを考慮して,与式の不等式を満たす単位円上の円弧の範囲を赤線で示す.
は単位円上の点の
成分に相当することを考慮して,与式の不等式を満たす単位円上の円弧の範囲を赤線で示す.
と赤色の円弧の部分が重なっている部分が答えとなる.よって,答えは
,
となる.
ホーム >> カテゴリー別分類 >> 三角関数 >> 三角関数の問題 >> 三角関数の不等式の問題 >>
三角関数の不等式の問題
最終更新日: 2025年9月10日