三角関数の方程式に関する問題

■問題

[　]内に示す範囲で，以下に示す方程式を解け．

$sin 2 θ = \frac{1}{2}$ 　 $[0 ≦ θ < π]$

$\frac{π}{12}, \frac{5}{12} π$

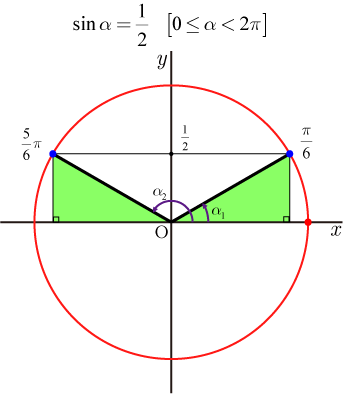
$2 θ = α$ 　･･････(1)

とおくと，与式は

$sin α = \frac{1}{2}$ 　･･････(2)

となる．

(1)の関係と $θ$ の範囲から， $α$ の範囲を求める．

$0 ≦ θ < π$

$0 ≦ 2 θ < 2 π$

よって

$0 ≦ α < 2 π$ 　･･････(3)

となる．

(2)を満たす $α$ を求める(図の $α_{1}$ ， $α_{2}$ の値)．

以下の問題を参考にする.

次の方程式を解け．ただし， $0 ≦ θ < 2 π$ とする．

$\sin θ = \frac{1}{2}$ 　⇒ 解

$α_{1} = \frac{π}{6}, α_{2} = \frac{5}{6} π$

(1)より $θ = \frac{1}{2} α$ なので，求める角をそれぞれ $θ_{1}, θ_{2}$ とすると

$θ_{1} = \frac{π}{12}, θ_{2} = \frac{5}{12} π$

となる．

学生スタッフ作成
最終更新日： 2025年2月6日