|
|||||||||||||
|
|||||||||||||
|
積分の問題(応用)
■問題
y=x+√x2+5 の逆関数を y=f(x) とする．
（１）f(x) を求めよ．
（２）定積分 ∫5√5f(x)dx を求めよ．
■答
（１）f(x)=x2−52x
（２）5−5log54
■解説
（１）y=x+√x2+5をx について解く．
y−x=√x2+5
ここで，y−x ＞0 に注意する．
両辺を2乗すると，
(y−x)2=(√x2+5)2
y2−2xy+x2=x2+5
xについて解くと，
y2−2xy+x2=x2+5
y2−2xy=5
−2xy=5−y2
x=−5−y22y=y2−52y ･･････(1)
ここで，y=x+√x2+5の定義域を考える．
y=x+√x2+5のグラフを以下に示す．
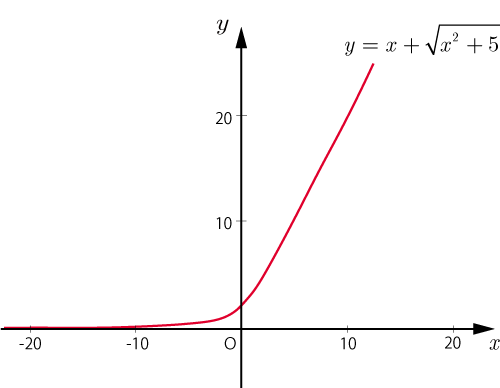
定義域：実数全体 （ちなみに値域は，y>0）
逆関数を求めるために(1)式のxとyを入れ替えると，
y=f(x)=x2−52x
逆関数y=x2−52x のグラフを以下に示す．
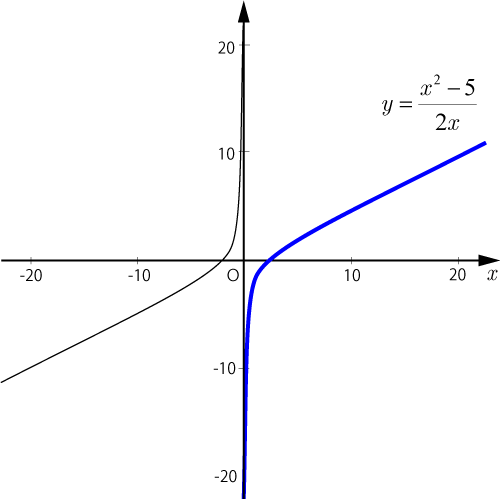
逆関数を求める際にxとyを入れ替えているので，逆関数の定義域は元の関数の値域になる．
よって，逆関数の定義域はx>0 となる．
（ちなみに値域は，実数全体）
y=f(x)=x2−52x
よって， y−x=√x2+5の逆関数は，(1)のxとyを入れ替えてy=x2−52xとなる(青線のグラフ)．
（２）（１）より，定積分∫5√5f(x)dxを求めると，
∫5√5f(x)dx
=∫5√5x2−52xdx
=∫5√5(x2−52x)dx
=[14x2−52logx]5√5
=14⋅52−52log5−(14⋅√52−52log√5)
=254−52log5−54+52log√5
=204−52log5+52log512
=5−52log5+12⋅52log5
=5−52log5+54log5
=5−5log54
ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>>y=x+√x2+5
最終更新日： 2023年11月24日
