定積分の問題

■問題

次の問題を積分せよ(定積分)．

${\displaystyle {\int }_{\frac{1}{2}}^1\sqrt{1-x^2}dx}$

■解説動画

◇積分の動画一覧のページへ

■答

${\displaystyle \frac{\pi }{6}-\frac{\sqrt{3}}{8}}$

■ヒント

定積分の基本式より

${\displaystyle {\int }_a^{b}f\left(x\right)dx={\left[F\left(x\right)\right]}_a^b=F\left(b\right)-F\left(a\right)}$

置換積分法より

${\displaystyle {\int }_a^{b}f\left(x\right)dx={\int }_{\alpha }^{\beta }f\left(g\left(t\right)\right)g^{\prime }\left(t\right)dt}$

を用いる．

この積分の計算は、図の赤色の面積を求める計算である．

■解説

● $x=\sin \theta$ とおいて置換積分する場合

あらかじめ， ${\displaystyle \int \sqrt{1-x^2}dx}$ を求めておく．

${\displaystyle x=sin\theta }$ ${\displaystyle \left(-\frac{\pi }{2}<\theta <\frac{\pi }{2}\right)}$ とおいて置換積分をする．（置換積分による解法を参照）

${\displaystyle \frac{dx}{d\theta }=cos\theta }$ ∴ ${\displaystyle dx=cos\theta d\theta }$

（ ${\displaystyle sin\theta }$ を微分すると ${\displaystyle cos\theta }$ になるのは， 微分 ${\displaystyle sinx}$ 　を参照）

${\displaystyle \int \sqrt{1-x^2}dx}$ ${\displaystyle =\int \sqrt{1-{sin}^2\theta }\cdot cos\theta d\theta }$

ここで，三角関数（三角比）の相互関係の ${\displaystyle 1}$ 番目の式  ${sin}^2\theta +{cos}^2\theta =1$ から

${\displaystyle \sqrt{1-{sin}^2\theta }=\sqrt{{cos}^2\theta }}$

${\displaystyle -\frac{\pi }{2}<\theta <\frac{\pi }{2}}$ より， ${\displaystyle cos\theta \geqq 0}$ →　 ${\displaystyle \sqrt{{cos}^2\theta }=cos\theta }$ である．

よって

${\displaystyle =\int {cos}^2\theta d\theta }$

ここで，半角の公式より（ ${\displaystyle {cos}^2\theta ={cos}^2\frac{2\theta }{2}}$ なので，半角の公式の ${\displaystyle \alpha }$ に ${\displaystyle 2\theta }$ を代入する）

${\displaystyle =\int \frac{1+cos2\theta }{2}d\theta }$

${\displaystyle =\frac{1}{2}\theta +\frac{1}{4}sin2\theta +C}$

（三角関数の積分を参照）
（これが ${\displaystyle \sqrt{1-x^2}}$ の原始関数である）

次に， ${\displaystyle {\int }_{\frac{1}{2}}^1\sqrt{1-x^2}dx}$ を求める．

はじめに ${\displaystyle x=sin\theta }$ と置換しているので

${\displaystyle x=\frac{1}{2}}$ のとき　 ${\displaystyle \theta =\frac{\pi }{6}}$ , ${\displaystyle x=1}$ のとき　 ${\displaystyle \theta =\frac{\pi }{2}}$

よって

${\displaystyle {\int }_{\frac{1}{2}}^1\sqrt{1-x^2}dx={\int }_{\frac{\pi }{6}}^{\frac{\pi }{2}}\frac{1+cos2\theta }{2}d\theta }$ ${\displaystyle ={\left[\frac{1}{2}\theta +\frac{1}{4}sin2\theta \right]}_{\frac{\pi }{6}}^{\frac{\pi }{2}}}$

（置換積分法を参照）

となる．

${\displaystyle ={\left[\frac{1}{2}\theta +\frac{1}{4}sin2\theta \right]}_{\frac{\pi }{6}}^{\frac{\pi }{2}}}$

${\displaystyle =\frac{1}{2}\cdot \frac{\pi }{2}+\frac{1}{4}sin\left(2\cdot \frac{\pi }{2}\right)}$ ${\displaystyle -\left\{\frac{1}{2}\cdot \frac{\pi }{6}+\frac{1}{4}sin\left(2\cdot \frac{\pi }{6}\right)\right\}}$

${\displaystyle =\frac{\pi }{4}+\frac{1}{4}\cdot sin\pi -\left(\frac{\pi }{12}+\frac{1}{4}sin\frac{\pi }{3}\right)}$

${\displaystyle =\frac{\pi }{4}+\frac{1}{4}\cdot 0-\frac{\pi }{12}-\frac{1}{4}\cdot \frac{\sqrt{3}}{2}}$

${\displaystyle =\frac{\pi }{6}-\frac{\sqrt{3}}{8}}$

上記置換積分の変数変換の考えを幾何学的に表したのが下図である．

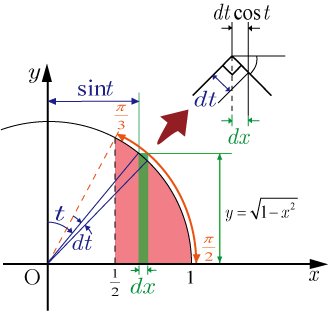
■解説

● $x=\cos \varphi$ とおいて置換積分する場合

${\displaystyle x=\cos \varphi }$ ${\displaystyle \left(0\leqq \varphi \leqq \pi \right)}$ とおく．

${\displaystyle \frac{dx}{d\varphi }=-\sin \varphi }$ より， ${\displaystyle dx=-\sin \varphi d\varphi }$

${\displaystyle x:\frac{1}{2}\to 1}$ のとき， ${\displaystyle \varphi :\frac{\pi }{3}\to 0}$

よって

${\displaystyle {{\displaystyle \int }}_{\frac{1}{2}}^1\sqrt{1-x^2}dx}$ ${\displaystyle ={{\displaystyle \int }}_{\frac{\pi }{3}}^0\sqrt{1-{\cos }^2\varphi }\left(-\sin \varphi \right)d\varphi }$

${\displaystyle {\sin }^2\varphi +{\cos }^2\varphi =1}$ の関係を用いると

${\displaystyle =-{{\displaystyle \int }}_{\frac{\pi }{3}}^0\sqrt{{\sin }^2\varphi }\sin \varphi d\varphi }$

${\displaystyle {\int }_a^{b}f\left(x\right)dx=-{\int }_b^{a}f\left(x\right)dx}$ ここを参照

${\displaystyle 0\leqq \varphi \leqq \pi }$ より ${\displaystyle \sin \varphi \geqq 0}$ ．よって， ${\displaystyle \sqrt{{\sin }^2\varphi }=\sin \varphi }$ ．

したがって

${\displaystyle ={{\displaystyle \int }}_0^{\frac{\pi }{3}}\sin \varphi \sin \varphi d\varphi }$

${\displaystyle ={{\displaystyle \int }}_0^{\frac{\pi }{3}}{\sin }^2\varphi d\varphi }$

半角の公式を用いると

${\displaystyle ={{\displaystyle \int }}_0^{\frac{\pi }{3}}\frac{1}{2}\left(1-\cos 2\varphi \right)d\varphi }$

${\displaystyle =\frac{1}{2}{\left[\varphi -\frac{1}{2}\sin 2\varphi \right]}_0^{\frac{\pi }{3}}}$

${\displaystyle =\frac{1}{2}\left\{\left(\frac{\pi }{3}-\frac{1}{2}\sin \frac{2\pi }{3}\right)-\left(0-\frac{1}{2}\sin 0\right)\right\}}$

${\displaystyle =\frac{1}{2}\left(\frac{\pi }{3}-\frac{1}{2}\cdot \frac{\sqrt{3}}{2}\right)}$

${\displaystyle =\frac{\pi }{6}-\frac{\sqrt{3}}{8}}$

上記置換積分の変数変換の考えを幾何学的に表したのが下図である．

●参考

求める面積は扇形 $\text{OAB}$ の面積から三角形 $\text{OBC}$ の面積を引いたものである．

扇形 $\text{OAB}$ の面積 ${\displaystyle =\pi \cdot 1^2\cdot \frac{\frac{\pi }{3}}{2\pi }=\frac{\pi }{6}}$

三角形 $\text{OBC}$ の面積 ${\displaystyle =\frac{1}{2}\cdot \frac{1}{2}\sin \frac{\pi }{3}=\frac{1}{4}\cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{8}}$

したがって

${\displaystyle {{\displaystyle \int }}_{\frac{1}{2}}^1\sqrt{1-x^2}dx}$ ${\displaystyle =\frac{\pi }{6}-\frac{\sqrt{3}}{8}}$

　

ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題 >> ${\displaystyle {\int }_{\frac{1}{2}}^1\sqrt{1-x^2}dx}$

学生スタッフ作成
最終更新日： 2025年6月9日