|
|||||||||||||
|
|||||||||||||
|
問題を解くのに必要な知識を確認するにはこの知識グラフを利用してください.
基本的な指数関数のグラフ
■問題
次の式のグラフを描け.
■答
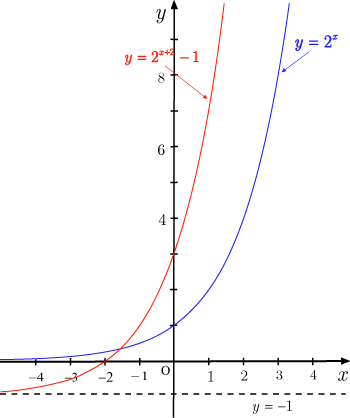
■ヒント
基本となるグラフを 平行移動することによって描く.
のグラフの場合,基本となるグラフは
である.
■解き方
関数のグラフを軸方向に,軸方向に平行移動したグラフを表す関数は
……
である.(グラフの平行移動参照)
を
と変形すると,では,がのに相当する.
すなわち
である.
であり,より軸方向の平行移動量に相当するのはとなる.
また
であり,より軸方向の平行移動量に相当するのはとなる.
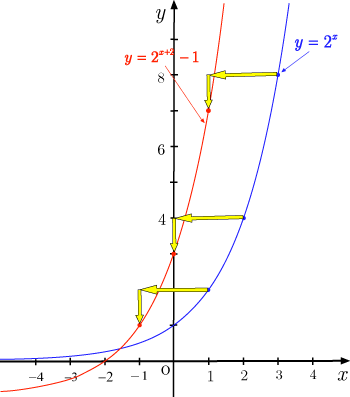
以上より
のグラフはのグラフを
軸方向に ,軸方向に
平行移動したものであることがわかる.
したがって,グラフは下図のようになる.
ホーム>>カテゴリー分類>>指数/対数>>指数に関する問題>>指数関数のグラフを描く問題
作成:学生スタッフ
最終更新日: 2023年11月29日