直交するベクトルを求める

■問題

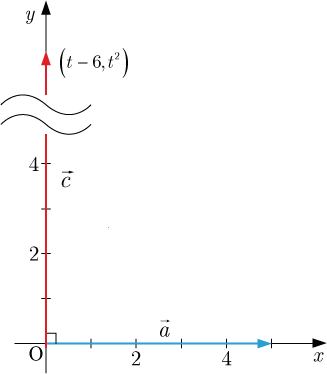
${\displaystyle \overrightarrow{a}=\left(5,0\right)}$ ， ${\displaystyle \overrightarrow{c}=\left(t-6,t^2\right)}$ とするとき， ${\displaystyle \overrightarrow{a}}$ と ${\displaystyle \overrightarrow{c}}$ が直交するような ${\displaystyle t}$ を求めよ．

■解説動画

◇ベクトルに関する動画一覧のページへ

■答

${\displaystyle t=6}$

■ヒント

直交することより，内積が ${\displaystyle 0}$ である．すなわち

${\displaystyle \overrightarrow{a}·\overrightarrow{c}=0}$

となるような $t$ を求める．　 

■解説

${\displaystyle \overrightarrow{a}·\overrightarrow{c}}$ ${\displaystyle =\left(5,0\right)\cdot \left(t-6,t^2\right)}$

${\displaystyle =5\times \left(t-6\right)+0\times t^2}$

${\displaystyle =5t-30}$

なので

${\displaystyle 5t-30=0}$

${\displaystyle t=6}$

■参考

${\displaystyle \overrightarrow{c}}$ の始点が原点のとき，$t$が変化したときの終点の軌跡を求める．

${\displaystyle \overrightarrow{c}=\left(t-6,t^2\right)=\left(x,y\right)}$

とおくと

${\displaystyle x=t-6}$　･･････(1)

${\displaystyle y=t^2}$　･･････(2)

となる．(1)，(2)より媒介変数の $t$を消去する．(1)より

${\displaystyle t=x+6}$　･･････(3)

(3)を(2)に代入する．

${\displaystyle y={\left(x+6\right)}^2}$　･･････(4)

(4)より，軌跡は頂点が ${\displaystyle \left(-6,0\right)}$ の下に凸の放物線である．

　

ホーム>>カテゴリー分類>>ベクトル>>ベクトルに関する問題>>著効するベクトルを求める問題

学生スタッフ
最終更新日： 2026年1月23日