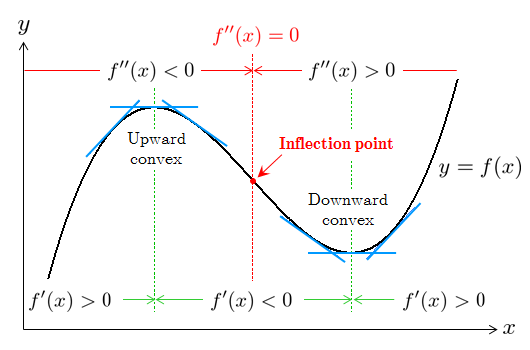
変曲点 (inflection point)

関数 $y = f (x)$ が $x$ のある区間で2次導関数 $f^{″} (x)$ をもち，この関数のグラフに凹凸があるとき，グラフの形が下に凸から上に凸（もしくは，上に凸から下に凸）に変わる点を変曲点 (inflection point) という．よって，変曲点では $f^{″} (x) = 0$ となっている．

「

$f^{″} (c) = 0$ となる点

$x = c$ の前後で

$f^{″} (x)$ の符号が反転していれば，点

$(c, f (c))$ は変曲点である．」

単に $f^{″} (c) = 0$ であっても，点 $(c, f (c))$ が変曲点であるとは限らない．変曲点かどうかは $x = c$ の前後で $f^{″} (x)$ の符号が正から負，あるいは負から正に変化しているか調べる必要がある．

■第2次導関数まで使った増減表

$x$	$\dots$	$α$	$\dots$	$c$	$\dots$	$β$	$\dots$
$f^{'} (x)$	$+$	$0$	$-$	$-$	$-$	$0$	$+$
$f^{″} (x)$	$-$	$-$	$-$	$0$	$+$	$+$	$+$
$f (x)$		極大値		$f (c)$		極小値

第2次導関数の増減表では，グラフの曲線の曲がり方も含めた矢印，，，を使う．

ホーム>>カテゴリー分類>>微分>>変曲点

最終更新日：2024年6月14日