関連するページを見るにはこのグラフ図を利用してください．

増減表

増減表とは，関数${\displaystyle y=f\left(x\right)}$  のグラフの概略を描くために，${\displaystyle f^{\prime }\left(x\right)}$  の符号を求めて関数${\displaystyle f\left(x\right)}$  の増加および減少の様子を表にまとめたものである．

上記の増減表からグラフの概略を描くと，下の図のようになる．

第2次導関数まで使った増減表⇒変曲点とグラフの凹凸を参照

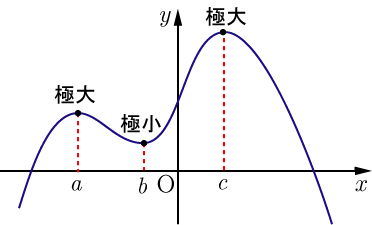
■増減表の書き方

関数$f\left(x\right)=x^3+3x^2-9x+5$  を例に増減表の一般的な書き方を説明する．

1. ${\displaystyle f^{\prime }\left(x\right)=0}$  を満たすx  の値を求める．（ ${\displaystyle f^{\prime }\left(x\right)=0}$  を満たすx  の値で関数${\displaystyle f\left(x\right)}$  は極大あるいは極小になる．）

   ${\displaystyle \begin{array}{ll}{f}^{\prime }\left(x\right)\hfill & =3x^2+6x-9\hfill \\ \hfill & =3\left(x^2+2x-3\right)\hfill \\ \hfill & =3\left(x+3\right)\left(x-1\right)\hfill \end{array}}$

   よって， ${\displaystyle f^{\prime }\left(x\right)=0}$  を満たすx  の値は，${\displaystyle x=-3,1}$  である． 求めた範囲で増減表を作成すると下のようになる．

   x	${\displaystyle \cdots }$	${\displaystyle -3}$	${\displaystyle \cdots }$	1	${\displaystyle \cdots }$
   ${\displaystyle f^{\prime }\left(x\right)}$		${\displaystyle 0}$		${\displaystyle 0}$
   ${\displaystyle f\left(x\right)}$

   
   
   
2. 次に，${\displaystyle f^{\prime }\left(x\right)}$ の符号と書き加え，${\displaystyle f\left(x\right)}$の増減を矢印で示す．（${\displaystyle f\left(x\right)>0}$  では関数${\displaystyle f\left(x\right)}$  は増加し，${\displaystyle f\left(x\right)<0}$  では関数${\displaystyle f\left(x\right)}$  は減少する．）

   x	${\displaystyle \cdots }$	${\displaystyle -3}$	${\displaystyle \cdots }$	1	${\displaystyle \cdots }$
   ${\displaystyle f^{\prime }\left(x\right)}$	+	${\displaystyle 0}$	-	${\displaystyle 0}$	+
   ${\displaystyle f\left(x\right)}$	${\displaystyle \nearrow }$		${\displaystyle \searrow }$		${\displaystyle \nearrow }$

   
   
   
3. 最後に極値の値を求める．

   ${\displaystyle f\left(-3\right)}$${\displaystyle ={\left(-3\right)}^3+3·{\left(-3\right)}^2-9·\left(-3\right)+5}$${\displaystyle =32}$

   ${\displaystyle f\left(1\right)}$${\displaystyle ={\left(1\right)}^3+3·{\left(1\right)}^2-9·\left(1\right)+5}$${\displaystyle =0}$

   x	${\displaystyle \cdots }$	−3	${\displaystyle \cdots }$	1	${\displaystyle \cdots }$
   ${\displaystyle f^{\prime }\left(x\right)}$	+	${\displaystyle 0}$	-	${\displaystyle 0}$	+
   ${\displaystyle f\left(x\right)}$	${\displaystyle \nearrow }$	${\displaystyle 32}$	${\displaystyle \searrow }$	${\displaystyle 0}$	${\displaystyle \nearrow }$

下に 関数$f\left(x\right)=x^3+3x^2-9x+5$   のグラフを示す．上の増減表と比較してみよう．

ホーム>>カテゴリー分類>>微分>>増減表

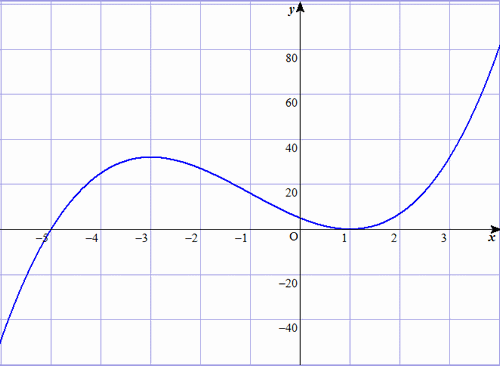
最終更新日： 2024年6月14日

[ページトップ]

利用規約

google translate (English version)