線分の内分点(複素平面)
複素数
,
に関して,複素平面上の点
と点
を結ぶ線分
を
に内分する点
の複素数
は
となる.
【参考】
■導出
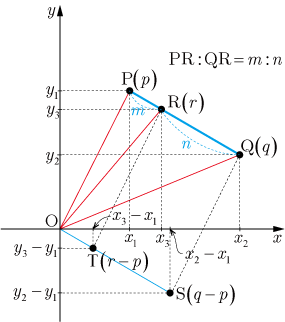
図1
線分
の長さは線分
の長さの
倍である.言い換えると,原点
と
点
を結ぶ線分
の長さは,原点
と
点
を結ぶ線分
の長さの
倍である.よって
となる.(複素数の実数倍を参照)
これより
・・・・・・(1)
が得られる.
(1)に
,
を代入すると
となる.
とおくと
となる.
ホーム>>カテゴリー分類>>複素数 >>内分点(複素平面)
最終更新日:
2025年11月25日