|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
問題リスト←このページに関連している問題です
2次方程式 の解き方
■解の公式による解き方
( の場合,判別式を参照)
■因数分解による解き方
まず下に示すように因数分解する(ここを参照).
→
これより,答えは
■考え方
・・・・・・(1)
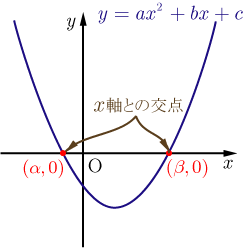
は2次関数
・・・・・・(2)
において の値が の場合に相当する.これをグラフで示すと,方程式(1)を満たす の値は, グラフ の 軸上の点に対応する.すなわち,方程式 の解 は, と 軸との交点の 座標の値と考えることができる.2次方程式(1)の解を とすると,(1)は因数定理と の係数が より,
・・・・・・(3)
と書きかえることができる.(3)式を展開すると,・・・・・・(4)
となる.(1)と(4)の係数を比較すると
・・・・・・(5)
・・・・・・(6)
の関係が得られる.これを解と係数の関係という.
(1)を(3)のように書き直すことができれば,2次方程式の解を求めることができる.
(1)を(3)のように書き直すと (式の変形はここを参照)
となる.よって,2次方程式 の解は
・・・・・・(8)
となる.(8)は2次方程式の解の公式である.
最終更新日: 2024年6月21日