アポロニウスの円

平面上の2点からの距離の比が一定の点の軌跡は円になり，その円のことをアポロニウスの円という．

■証明1

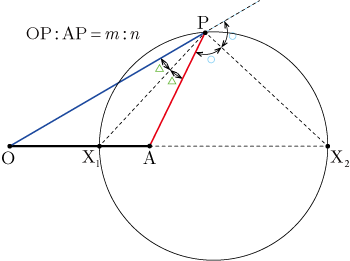
平面上の2点を，点$\text{O}$と点$\text{A}$とする（図を参照）．さらに，点$\text{P}$があり，点$\text{P}$，点$\text{O}$，点$\text{A}$の関係は

${\displaystyle \text{OP}:\text{AP}=m:n}$

となっている．

$△\text{OAP}$に関して

頂点$\text{A}$ の内角の二等分線と辺$\text{OA}$の交点を${\text{X}}_1$ とすると，点${\text{X}}_1$は辺$\text{OA}$の内分点になる．

頂点$\text{A}$の 外角の二等分線と辺$\text{OA}$の延長線との交点を${\text{X}}_2$ とすると，点${\text{X}}_2$ は辺$\text{OA}$の外分点になる．

${\displaystyle \angle {\text{X}}_1{\text{PX}}_2=90°}$ となることより，$m:n$が一定であれば，円周角の定理より

点 $\text{P}$の軌跡は，線分${\displaystyle {\text{X}}_1{\text{X}}_2}$を直径とする円

を描く

■証明2

座標平面を使って証明する．

２点の内１つは原点 $\text{O}$ とし，もう一方の点の座標を $\left(a,0\right)$ とし点 $\text{A}$ とする．ただし， ${\displaystyle a>0}$ とする．そして， $\text{OP}:\text{OA}=m:n$ となる点 $\text{P}$ の座標を ${\displaystyle \left(x,y\right)}$ とする．

上記内容を式で表すと

${\displaystyle \sqrt{x^2+y^2}:\sqrt{{\left(x-a\right)}^2+y^2}=m:n}$ ･･････(1)

となる．この式を以下のように変形する．

${\displaystyle n\sqrt{x^2+y^2}=m\sqrt{{\left(x-a\right)}^2+y^2}}$

${\displaystyle n^2\left(x^2+y^2\right)=m^2\left\{{\left(x-a\right)}^2+y^2\right\}}$

${\displaystyle n^2{x}^2+n^2{y}^2}$ ${\displaystyle =m^2{x}^2-2m^{2}ax+m^2{a}^2+m^2{y}^2}$

${\displaystyle \left(n^2-m^2\right)x^2+2m^{2}ax+\left(n^2-m^2\right)y^2}$ ${\displaystyle =m^2{a}^2}$

${\displaystyle x^2+\frac{2m^{2}a}{n^2-m^2}x+y^2}$ ${\displaystyle =\frac{m^2{a}^2}{n^2-m^2}}$

${\displaystyle {\left\{x+\frac{m^{2}a}{n^2-m^2}\right\}}^2+y^2}$ ${\displaystyle =\frac{m^2{a}^2}{n^2-m^2}+{\left\{\frac{m^{2}a}{n^2-m^2}\right\}}^2}$

${\displaystyle {\left\{x+\frac{m^{2}a}{n^2-m^2}\right\}}^2+y^2}$ ${\displaystyle =\frac{m^2{a}^2\left(n^2-m^2\right)+m^4{a}^2}{{\left(n^2-m^2\right)}^2}}$

${\displaystyle {\left\{x+\frac{m^{2}a}{n^2-m^2}\right\}}^2+y^2}$ ${\displaystyle =\frac{m^2{n}^2{a}^2}{{\left(n^2-m^2\right)}^2}}$

${\displaystyle {\left\{x+\frac{m^{2}a}{n^2-m^2}\right\}}^2+y^2}$ ${\displaystyle ={\left(\frac{mna}{n^2-m^2}\right)}^2}$ ･･････(2)

(2)は円の方程式で，円の中心が， ${\displaystyle \left(-\frac{m^{2}a}{n^2-m^2},0\right)}$ ，半径が， ${\displaystyle \frac{mna}{\left|n^2-m^2\right|}}$ の円を表す．

円の $x$ 軸との交点を求めてみる．(2)に $y=0$ を代入する．

${\displaystyle {\left\{x+\frac{m^{2}a}{n^2-m^2}\right\}}^2={\left(\frac{mna}{n^2-m^2}\right)}^2}$

${\displaystyle x^2+\frac{2m^{2}a}{n^2-m^2}x+{\left(\frac{m^{2}a}{n^2-m^2}\right)}^2-{\left(\frac{mna}{n^2-m^2}\right)}^2=0}$

${\displaystyle x^2+\frac{2m^{2}a}{n^2-m^2}x+\frac{m^4{a}^2-m^2{n}^2{a}^2}{{\left(n^2-m^2\right)}^2}=0}$

${\displaystyle x^2+\frac{2m^{2}a}{n^2-m^2}x+\frac{m^2{a}^2\left(m^2-n^2\right)}{{\left(n^2-m^2\right)}^2}=0}$

${\displaystyle x^2+\frac{2m^{2}a}{n^2-m^2}x-\frac{m^2{a}^2}{n^2-m^2}=0}$

解の公式より

${\displaystyle x=-\frac{m^{2}a}{n^2-m^2}\pm \sqrt{{\left\{\frac{m^{2}a}{\left(n^2-m^2\right)}\right\}}^2+\frac{m^2{a}^2}{n^2-m^2}}}$

${\displaystyle =-\frac{m^{2}a}{n^2-m^2}\pm \sqrt{\frac{m^4{a}^2+m^2{a}^2\left(n^2-m^2\right)}{{\left(n^2-m^2\right)}^2}}}$

${\displaystyle =-\frac{m^{2}a}{n^2-m^2}\pm \sqrt{\frac{m^2{n}^2{a}^2}{{\left(n^2-m^2\right)}^2}}}$

${\displaystyle =-\frac{m^{2}a}{n^2-m^2}\pm \frac{mna}{\left|n^2-m^2\right|}}$　･･････(2)

${\displaystyle =-\frac{m^{2}a}{n^2-m^2}\pm \frac{mna}{n^2-m^2{}^2}}$

${\displaystyle =-\frac{m^{2}a\mp mna}{n^2-m^2}}$

${\displaystyle =-\frac{ma\left(m\mp n\right)}{n^2-m^2}}$

${\displaystyle =\frac{ma\left(m\mp n\right)}{m^2-n^2}}$

${\displaystyle =\frac{ma\left(m-n\right)}{\left(n-m\right)\left(n+m\right)}}$ ，${\displaystyle \frac{ma\left(m+n\right)}{\left(n-m\right)\left(n+m\right)}}$

${\displaystyle =\frac{ma}{m+n},\frac{ma}{m-n}}$

よって，円と$x$軸との交点の座標は

${\displaystyle \left(\frac{ma}{m+n},0\right)}$ ，${\displaystyle \left(\frac{ma}{m-n},0\right)}$

となる．

点${\displaystyle \left(\frac{ma}{m+n},0\right)}$は，線分$\text{OA}$を${\displaystyle m:n}$ に内分した点であり，点 ${\displaystyle \left(\frac{ma}{m-n},0\right)}$ は，線分$\text{OA}$を${\displaystyle m:n}$に外分した点である．

$m$，$n$の値をスライダーの〇印をドラグして変更してみてください．また，点$\text{P}$をドラッグして動かしてみてください．

 

ホーム>>カテゴリー分類>>幾何>>アポロニウスの円

最終更新日 ： 2025年11月25日

[ページトップ]

利用規約

google translate (English version)