関連するページを見るにはこのグラフ図を利用してください．

円錐曲線 (conic curve)

円錐を任意の平面で切断したとき，その切り口に現れる曲線を 円錐曲線 (conic curve) という．切断する平面の角度によって，曲線は円 (circle)，楕円 (ellipse)，放物線 (parabola)，双曲線 (hyperbola)に分けられる（分類上，円は楕円に含まれる）．

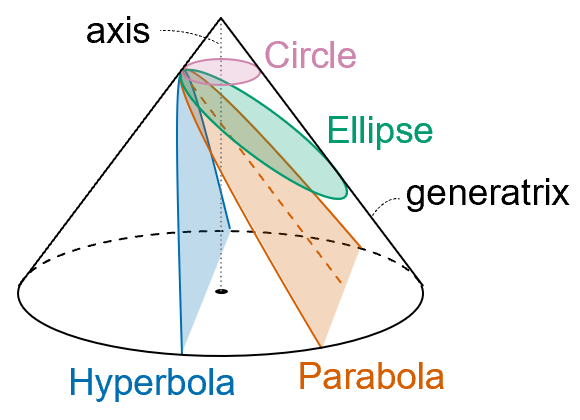
円錐の頂点 (vertex)から底面の円周上の点を結ぶ線分を，その円錐の母線 (generatrix)といい，円錐の母線と円錐の軸 (axis)とのなす角を ${\displaystyle \theta }$ とする．また，円錐切断面と円錐の軸とのなす角を ${\displaystyle \varphi }$ とする．このとき，以下の関係により現れる曲線が決まる．

• 円 (circle)    ${\displaystyle \iff }$    ${\displaystyle \varphi =90°}$
  切断面が円錐の軸と垂直になる．


• 楕円 (ellipse)    ${\displaystyle \iff }$    ${\displaystyle \theta <\varphi <90°}$
  切断面と円錐軸とのなす角が，母線と軸とのなす角よりも大きい（切断面が対の円錐の片方のみと交わる）．


• 放物線 (parabola)    ${\displaystyle \iff }$    ${\displaystyle \varphi =\theta }$
  切断面が円錐の母線と平行になる．


• 双曲線 (hyperbola)    ${\displaystyle \iff }$    ${\displaystyle \varphi <\theta }$
  切断面と円錐軸とのなす角が，母線と軸とのなす角よりも小さい（切断面が対の円錐の両方と交わる）．

これらの円錐曲線は， ${\displaystyle xy}$ 平面において， ${\displaystyle x}$ と ${\displaystyle y}$ についての2次式で表されるため，2次曲線ともいう．

通常，円錐を切断する平面は円錐の頂点を通らないことを想定するために上記の円錐曲線（楕円・放物線・双曲線）が得られるが，円錐の頂点を通る平面で切断すると，その切り口に現れる図形は点または直線となる．この特別な場合の図形を退化円錐 (degenerate conic)という．

ホーム>>カテゴリー分類>>幾何>>図と方程式>>円錐曲線

最終更新日：2025年10月24日

[ページトップ]

利用規約

google translate (English version)