積和の公式
⇒公式の導出
⇒公式の導出
⇒公式の導出
⇒公式の導出
■解説動画
■積和の公式の導出
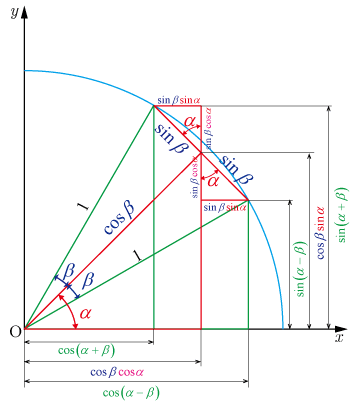 ●
の導出
●
の導出
sinの加法定理より
・・・・・・(1)
・・・・・・(2)
である.(1)+(2)より
・・・・・・(3)
(3)を変形して
が得られる.
●
の導出
sinの加法定理より
・・・・・・(1)
・・・・・・(2)
である.(1)ー(2)より
・・・・・・(4)
(4)を変形して
が得られる.
●
の導出
cosの加法定理より
・・・・・・(5)
・・・・・・(6)
である.(5)+(6)より
・・・・・・(7)
(7)を変形して
が得られる.
●
の導出
cosの加法定理より
・・・・・・(5)
・・・・・・(6)
である.(5)−(6)より,
・・・・・・(8)
(8)を変形して
が得られる.
ホーム>>カテゴリー分類>>三角関数>>積和の公式
最終更新日
2025年8月25日
 ●
の導出
●
の導出