曲線の長さ
媒介変数表示された曲線 , の長さ は
曲線 , の長さ は
となる.ただし,
,
である.
■関連動画
■導出
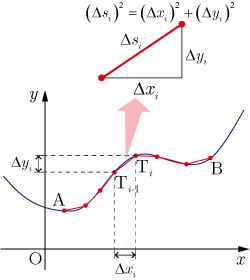 関数,は閉区間 で定義されている.この区間 をとなるで 個の区間に分割する. , ,とすると, は曲線上にある.(右図参照) 線分の長さ
は, , , , ,とすると
関数,は閉区間 で定義されている.この区間 をとなるで 個の区間に分割する. , ,とすると, は曲線上にある.(右図参照) 線分の長さ
は, , , , ,とすると
曲線の長さは,和の極限としての定積分の考え方より
となる. 一方
と考えると,曲線 の長さは
となりる.
以上より,公式が導かれる.(区分求積法を参考する)
ホーム>>カテゴリー分類>>積分 >>定積分の定義>>曲線の長さ
最終更新日:
2024年5月17日