平行六面体の体積

${\displaystyle \overrightarrow{a_1}}$ ， ${\displaystyle \overrightarrow{a_2}}$ ， ${\displaystyle \overrightarrow{a_3}}$ を3辺とする平行六面体の体積 $V$ は

${\displaystyle V=\left|\overrightarrow{a_1}\cdot \left(\overrightarrow{a_2}\times \overrightarrow{a_3}\right)\right|}$ ･･････(1)

となる．

■導出

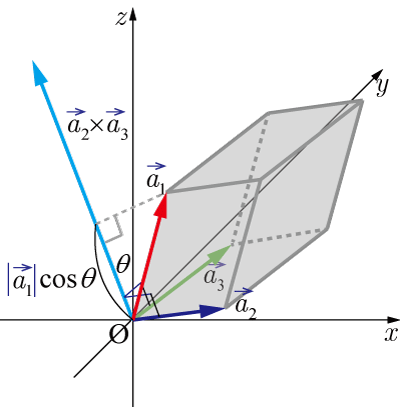
図のような平行六面体を考える.

${\displaystyle \overrightarrow{a_2}}$ と ${\displaystyle \overrightarrow{a_3}}$ を2辺とする平行四辺形を平行六面体の底面とする．底面の面積 $S$ は，外積の定義より

${\displaystyle S=\left|\overrightarrow{a_2}\times \overrightarrow{a_3}\right|}$ ･･････(2)

となる．

${\displaystyle \overrightarrow{a_2}\times \overrightarrow{a_3}}$ のベクトルは底面と垂直な関係である． ${\displaystyle \overrightarrow{a_1}}$ と ${\displaystyle \overrightarrow{a_2}\times \overrightarrow{a_3}}$ のなす角を ${\displaystyle \theta }$ とすると，平行六面体の高さ $h$ は

${\displaystyle h=\left|\overrightarrow{a_1}\right|\left|\cos \theta \right|}$ ･･････(3)

（ ${\displaystyle \overrightarrow{a_1}}$ ， ${\displaystyle \overrightarrow{a_2}}$ ， ${\displaystyle \overrightarrow{a_3}}$ の位置関係によっては， ${\displaystyle 90°<\theta <180°}$ となり， ${\displaystyle \cos \theta <0}$ の場合もあるので， ${\displaystyle \cos \theta }$ の絶対値を取っている）

となる．

(2)，(3)より，平行六面体の体積$V$は

${\displaystyle V=Sh}$

${\displaystyle =\left|\overrightarrow{a_2}\times \overrightarrow{a_3}\right|\left|\overrightarrow{a_1}\right|\left|\cos \theta \right|}$

${\displaystyle =\left|\left|\overrightarrow{a_2}\times \overrightarrow{a_3}\right|\left|\overrightarrow{a_1}\right|\cos \theta \right|}$

（${\displaystyle \left|\overrightarrow{a_2}\times \overrightarrow{a_3}\right|\left|\overrightarrow{a_1}\right|\cos \theta }$ の絶対値を取っている）

内積の定義より式を変形する

${\displaystyle =\left|\left(\overrightarrow{a_2}\times \overrightarrow{a_3}\right)\cdot \overrightarrow{a_1}\right|}$

内積は交換法則が成り立つことより

${\displaystyle =\left|\overrightarrow{a_1}\cdot \left(\overrightarrow{a_2}\times \overrightarrow{a_3}\right)\right|}$

となる．

実際の計算は，3次の行列式の幾何学的解釈を参考にするとよい．

【備考】${\displaystyle \overrightarrow{a_1}\cdot \left(\overrightarrow{a_2}\times \overrightarrow{a_3}\right)}$ のことをスカラー3重積という．