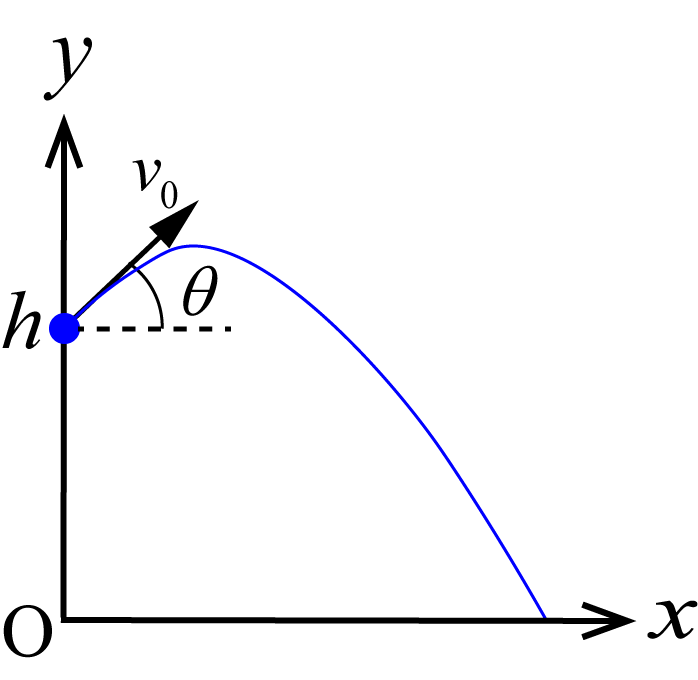
ある高度からの斜方投射
図のように，質量
m [
kg ]
の小球を，地上から高さ
h [ m ]
のところから，水平面から角度
θ
の方向に，速さ
v
0
[
m/s ]
で斜方投射した．ただし，重力加速度の大きさを
g [
m/s
2
]
として，空気抵抗は無視する．
(1)
運動方程式を立てよ．ただし加速度ベクトルを
d
2
d
t
2
(
x,y
)
とする．
解答
m
d
2
d
t
2
(
x,y
)=(
0,−mg
)
閉じる
解説
斜方投射では投げられた後の物体には鉛直下向きの重力(
−mg
)しか働かない．
したがって，
x
軸方向に等速直線運動，
y
軸方向に等加速度直線運動(鉛直投げ上げと同じ運動)をする．
よって
運動方程式は
水平方向：
m
d
2
x
d
t
2
=0
，
鉛直方向：
m
d
2
y
d
t
2
=−mg
より，
m
d
2
d
t
2
(
x,y
)=(
0,−mg
)
となる．
閉じる
(2)
最高点に達する時間
t
top
を求めよ．
解答
t
top
=
v
0
sinθ
g
[ s ]
閉じる
解説
初速
v
0
を図のように
x,y
成分に分解して考えると，
y
軸方向の速度は
v
0
sinθ
と表される．放物運動は，各軸方向の運動を独立に考えればよいので，鉛直方向の鉛直投げ上げについて考える．
運動方程式を解くと，
a=−g
となり，小球は等加速度直線運動をしていることが分かる．
したがって，等加速度直線運動の式より任意の時刻
t
[ s ]
における小球の速度
v
y
は次のように表すことができる．
v
y
=
v
0
sinθ+at=
v
0
sinθ−gt
投げ上げた小球が最高点に到達したとき，速度は
0 m/s
となるので，そのときの時刻を
t
top
[ s ]
とすると，
0=
v
0
sinθ−g
t
top
となる．
よって，
g
t
top
=
v
0
sinθ
t
top
=
v
0
sinθ
g
となる．
閉じる
(3)
最高点の高さ
y
top
を求めよ．
解答
y
top
=h+
v
0
2
sin
2
θ
2g
[ m ]
閉じる
解説
最高点の高さは，等加速度直線運動の式
y=
y
0
+
v
0
t+
1
2
a
t
2
に小球の初期位置
y
0
=h [ m ]
と
y
軸方向の初速
v
0
sinθ [
m/s ]
，加速度
a=−g[
m/s
2
]
，(2)の解である最高点に達する時間
t
top
=
v
0
sinθ
g
を代入することで求められる．
つまり，
y
top
(
t
top
)=h+
v
0
sinθ
v
0
sinθ
g
+
1
2
⋅(
−g
)⋅
(
v
0
sinθ
g
)
2
=h+
v
0
sinθ
v
0
sinθ
g
−
1
2
g
v
0
2
sin
2
θ
g
2
=h+
2
v
0
2
sin
2
θ
2g
−
1
2
v
0
2
sin
2
θ
g
=h+
2
v
0
2
sin
2
θ−
v
0
2
sin
2
θ
2g
=h+
v
0
2
sin
2
θ
2g
[ m ]
閉じる
(4)
地上に達するまでの時間
t
1
を求めよ．
解答
t
1
=
v
0
sinθ+
v
0
2
sin
2
θ+2gh
g
閉じる
解説
等加速度直線運動の式
y=
y
0
+
v
0
t+
1
2
a
t
2
を用いることで落下にかかる時間を求めることができる．
つまり，原点
O
に達する時刻
t
1
のとき
y=0
となるので，
y
0
=h, a=−g
,
y
軸方向の初速
v
0
sinθ
も代入して，
0=h+
v
0
sinθ
t
1
−
1
2
g
t
1
2
g
t
1
2
−2
v
0
sinθ
t
1
−2h=0
解の公式を用いて2次方程式を解くと，
t
1
=
2
v
0
sinθ±
2
2
v
0
2
sin
2
θ−4g⋅(
−2h
)
2g
=
2
v
0
sinθ±
2
2
(
v
0
2
sin
2
θ+2gh
)
2g
=
2
v
0
sinθ±2
v
0
2
sin
2
θ+2gh
2g
=
v
0
sinθ±
v
0
2
sin
2
θ+2gh
g
g>0, h>0
なので
v
0
sinθ<
v
0
2
sin
2
θ+2gh
より，
v
0
sinθ−
v
0
2
sin
2
θ+2gh
g
<0
となってしまう．
したがって，
t
1
>0
となる解は
t
1
=
v
0
sinθ+
v
0
2
sin
2
θ+2gh
g
[ s ]
のみである．
閉じる
(5)
地上に達する直前の速さ
v
1
を求めよ．
解答
解説
水平方向は等速直線運動なので，任意の時刻において水平方向の速度は一定で，
v
x
=
v
0
cosθ
垂直方向は等速直線運動なので，等加速度直線運動の式
v=
v
0
+at
に原点
O
に達する直前の速度を
v
y
として，そのときの時刻
t
1
と
y
軸方向の初速
v
0
sinθ
を代入すると，
a=−g
より
v
y
=
v
0
sinθ−g
t
1
=
v
0
sinθ−g⋅
v
0
sinθ+
v
0
2
sin
2
θ+2gh
g
=
v
0
sinθ−
v
0
sinθ−
v
0
2
sin
2
θ+2gh
=−
v
0
2
sin
2
θ+2gh
[
m/s ]
よって，原点
O
に達する直前の速さ(速度ベクトルの大きさ)は
v
1
=
v
x
2
+
v
y
2
=
(
v
0
cosθ
)
2
+
(
v
0
2
sin
2
θ+2gh
)
2
=
v
0
2
cos
2
θ+
v
0
2
sin
2
θ+2gh
=
v
0
2
(
sin
2
θ+
cos
2
θ
)+2gh
sin
2
θ+
cos
2
θ=1
より，
v
1
=
v
0
2
+2gh
【別解】
この運動の間，小球に加わる外力は(保存力の)重力だけであり，非保存力である空気抵抗は十分に小さく無視できるものとしているため，力学的エネルギー保存の法則が成立する．
投げ上げた直後の力学的エネルギーは次のようになる．
mgh+
1
2
m
v
0
2
ただし，力学的エネルギー保存の法則では速さを用いるため，
x,y
成分に分解する前の
v
0
を使うことに注意する．
これと原点
O
に達する直前の(
y=0
)の力学的エネルギー
mg×0+
1
2
m
v
1
2
が等しくなる．
mgh+
1
2
m
v
0
2
=
1
2
m
v
1
2
gh+
1
2
v
0
2
=
1
2
v
1
2
v
1
2
=
v
0
2
+2gh
よって，速さは速度の大きさだから
v
1
>0
より，
v
1
=
v
0
2
+2gh
[
m/s ]
閉じる
ホーム>>物理演習問題>>力学>>質点の力学>>放物運動>>ある高度からの斜方投射
学生スタッフ作成
2020年9月17日
