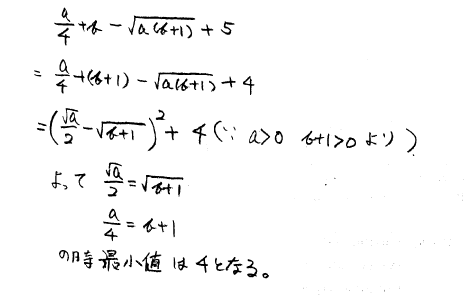【質問/問題】
下記の問題で私なりの解答を考えたのですが，
問題の解答とは値が異なってしまっています．
問題の解答も理解できるのですが，なぜ，私の解答が
間違っているのか分りません．どうかよろしくお願いします．

a>0,b>0の時　a/4+b-(a(b+1))^(1/2)+5の最小値を求めよ．

【私の解答】
　a>0,b>0より，相加・相乗平均の公式を使うと
　　a/4+b>=2(ab/4)^(1/2) ・・・�@
等号成立はa/4=bの時

　また，a>0,b+1>0より，相加・相乗平均の公式を使うと
a+(b+1)>=2(a(b+1))^(1/2)　　・・・�A
　　等号成立はa=b+1の時

�@,�Aより
（与式）>=(ab)^(1/2)-(a+b+1)/2+5・・・�D
等号成立はa/4=b・・・�B且つa=b+1・・・�Cの時

�B,�Cより
a=4/3,b=1/3
a=4/3,b=1/3を�Dに代入すると最小値が求まる
（与式の最小値）＝2/3-(4/3+1/3+1)/2+5=13/3

【問題の解答】
　a/4>0,b+1>0より，相加・相乗平均の公式を使うと
　　a/4+b+1>=2(a(b+1)/4)^(1/2) ・・・�@
等号成立はa/4=b+1の時
�@より
（与式）>=(a(b+1))^(1/2)-a(b+1))^(1/2)+4=4

よって，最小値は４である．

【解答】

間違えているところは，

等号成立はa/4=b・・・�B且つa=b+1・・・�Cの時

です．�Bと�Cが同時に成立することはありません．�Cを�Bに代入すると方程式が成り立たないことが分かるはずです．

以下の式の変形を参考にしてください．