問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

定義域、値域、変化量に関する問題

■問題

関数 ${\displaystyle y=\frac{1}{x-2}}$ について，定義域と値域を答え，さらに $x$ が $a$ から ${\displaystyle a+1}$ まで変化したとき 関数の値の変化量 ${\displaystyle \Delta y}$ を求めよ．${\displaystyle f\left(x\right)=\frac{1}{x-2}}$ とおくと，${\displaystyle \Delta y=f\left(a+1\right)-f\left(a\right)}$ となる．

■答

定義域：$x=2$ を除く実数全体（または，$x\ne 2$ の実数全体）

値域：$y=0$ を除く実数全体（または，$y\ne 0$ の実数全体）

${\displaystyle f\left(a+1\right)-f\left(a\right)}$${\displaystyle =-\frac{1}{\left(a-1\right)\left(a-2\right)}}$

■解説

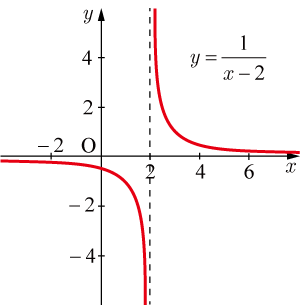
${\displaystyle y=\frac{1}{x-2}}$ のグラフは ${\displaystyle y=\frac{1}{x}}$のグラフを $x$ 軸方向に $2$ へ平行移動したもので図のようになる． $x$ 軸と直線 $x=2$ が漸近線となっている．

となる．

グラフより

定義域は，$x=2$ を除く実数全体（または，$x\ne 2$ の実数全体）

値域は，$y=0$ を除く実数全体（または，$y\ne 0$ の実数全体）

となる．

${\displaystyle f\left(a+1\right)-f\left(a\right)}$${\displaystyle =\frac{1}{\left(a+1\right)-2}-\frac{1}{a-2}}$

${\displaystyle =\frac{1}{a-1}-\frac{1}{a-2}}$

通分する．

${\displaystyle =\frac{\left(a-2\right)-\left(a-1\right)}{\left(a-1\right)\left(a-2\right)}}$

${\displaystyle =\frac{a-2-a+1}{\left(a-1\right)\left(a-2\right)}}$

${\displaystyle =\frac{-1}{\left(a-1\right)\left(a-2\right)}}$

${\displaystyle =-\frac{1}{\left(a-1\right)\left(a-2\right)}}$

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>1次関数，2次関数などに関する問題>>定義域，値域，変化量に関する問題

最終更新日： 2024年9月13日

[ページトップ]

利用規約

google translate (English version)