問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

方程式の解の存在に関する問題

■問題

解の存在定理を用いて，方程式 ${\displaystyle 3^x=6x-1}$ が ， ${\displaystyle 0<x<1}$ の区間に実数解を持つことを示せ．

■ヒント

方程式の実数解の存在定理

■答

${\displaystyle f\left(x\right)=3^x-6x+1}$と置く．

指数関数${\displaystyle 3^x}$ と一次関数 ${\displaystyle 6x-1}$ の差から成る関数 ${\displaystyle f\left(x\right)}$ は実数全体で連続である．よって

${\displaystyle f\left(x\right)}$は，${\displaystyle 0<x<1}$ の区間で連続である　･･････(1)

また

${\displaystyle f\left(0\right)=3^0-6\cdot 0+1}$${\displaystyle =1-0+1}$${\displaystyle =2}$　･･････(2)

${\displaystyle f\left(1\right)=3^1-6\cdot 1+1}$${\displaystyle =3-6+1}$${\displaystyle =-2}$　･･････(3)

(1)，(2)より

${\displaystyle f\left(0\right)\cdot f\left(1\right)=2\cdot \left(-2\right)=-4<0}$　･･････(4)

である．

(1)と(4)，および，方程式の実数解の存在定理より

方程式 ${\displaystyle 3^x=6x-1}$ は ， ${\displaystyle 0<x<1}$ の区間に少なくとも1つ実数解を持つ

ことになる．

 

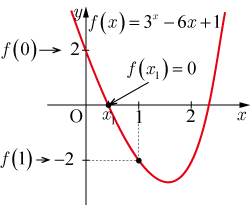
ホーム>>カテゴリー分類>>関数>>関数の演習問題>>いろいろな方程式に関する問題>>方程式の解の存在に関する問題

最終更新日： 2024年9月13日

[ページトップ]

利用規約

google translate (English version)