関連するページを見るにはこのグラフ図を利用してください．

微分係数

関数 ${\displaystyle f\left(x\right)}$ の ${\displaystyle x=a}$ における微分係数とは，平均変化率の式で $h$ を限りなく0に近づけた時の値で， ${\displaystyle f^{\prime }\left(a\right)}$ と表わす．すなわち，

${\displaystyle f^{\prime }\left(a\right)=\underset{h\to 0}{lim}\frac{f\left(a+h\right)-f\left(a\right)}{h}}$

である．また，

${\displaystyle f^{\prime }\left(a\right)=\underset{b\to a}{lim}\frac{f\left(b\right)-f\left(a\right)}{b-a}}$

と表すこともできる．

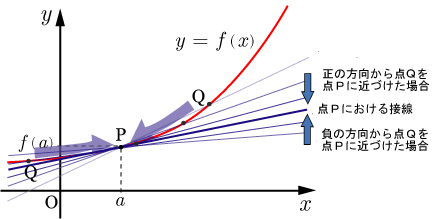
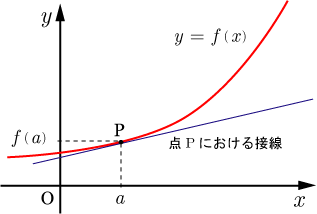
上の微分係数の定義式を，下図を用いて説明する． $h$ を限りなく0に近づけることは，点Qを点Pに限りなく近づけることと同じである．点Qを点Pに限りなく近づけていくと，直線PQの傾き（平均変化率）はある値に近づく．その値が ${\displaystyle x=a}$ における微分係数である．いいかえると，関数 ${\displaystyle f\left(x\right)}$ の ${\displaystyle x=a}$ における接線の傾きになる．

 

■具体例

関数 ${\displaystyle f\left(x\right)=x^2}$ の ${\displaystyle x=2}$ における微分係数を求めてみる．

下の表は $x$ の値が2から2+ $h$ に変化したときの平均変化率の値を求めている． $h$ の値が0に近づくにつれてある値（4）に近づいていることがわかる．

• 正の方向から2に近づけた場合
  $h$	平均変化率
  2	6
  1	5
  0.5	4.5
  0.25	4.25
  0.125	4.125
  0.0625	4.0625
  0.03125	4.03125
  0.015625	4.015625
  0.0078125	4.0078125
  0.00390625	4.00390625
  0.001953125	4.001953125

• 負の方向から2に近づけた場合
  $h$	平均変化率
  -2	2
  -1	3
  -0.5	3.5
  -0.25	3.75
  -0.125	3.875
  -0.0625	3.9375
  -0.03125	3.96875
  -0.015625	3.984375
  -0.0078125	3.9921875
  -0.00390625	3.99609375
  -0.001953125	3.998046875

次に，微分係数の定義式にしたがって計算してみる．

${\displaystyle \begin{array}{ll}{f}^{\prime }\left(2\right)\hfill & =\underset{h\to 0}{lim}\frac{f\left(2+h\right)-f\left(2\right)}{h}\hfill \\ \hfill & =\underset{h\to 0}{lim}\frac{{\left(2+h\right)}^2-2^2}{h}\hfill \\ \hfill & =\underset{h\to 0}{lim}\frac{4+4h+h^2-4}{h}\hfill \\ \hfill & =\underset{h\to 0}{lim}\frac{4h+h^2}{h}\hfill \\ \hfill & =\underset{h\to 0}{lim}\left(4+h\right)\hfill \\ \hfill & =4\hfill \end{array}}$

${\displaystyle x=2}$ における微分係数は4であることがわかる．

 

ホーム>>カテゴリー分類>>微分>>微分係数

最終更新日： 2025年2月21日

[ページトップ]

利用規約

google translate (English version)