関連するページを見るにはこのグラフ図を利用してください．

関数

ある値 xに対して，ただ1つの値yが対応するような関係があるとき，この関係を関数といい，一般的に

${\displaystyle y=f\left(x\right)}$

と表す．また，yはxの関数であるという．この場合，関数を表す文字としてf  を一般的に用いたが， gやhなど他の文字を用いることもよく使われる．

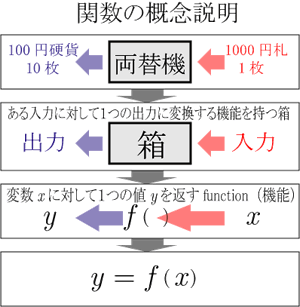
このような関数の概念を説明したのが右の図である．

両替機を例にとる．1000札1枚を両替機に入れる（入力する）と100円硬貨が10枚でる（出力される）．すなわち，両替機は入力に対して1つの出力が決まっている関数機能がある機械である．同じように，ある値x（xを変数と呼ぶ）に対して1つの値yに対応させる機能を文字で表すと一般的に，${\displaystyle y=f\left(x\right)}$となる．

関数${\displaystyle y=f\left(x\right)}$において，xの値aに対応するyの値を${\displaystyle f\left(a\right)}$  と表し，これを関数${\displaystyle f\left(x\right)}$ の${\displaystyle x=a}$における値という．

${\displaystyle f\left(x\right)}$の関数（機能）を具体的に表すとする．例えば，長さ20のひもで長方形を作る場合，横の長さxを決めて縦の長さを対応させる関数は

${\displaystyle f\left(x\right)=10-x}$

のように表す．あるいは

${\displaystyle y=10-x}$

と表してもよい．

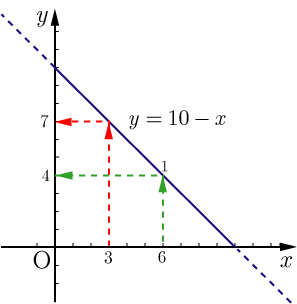
　${\displaystyle y=10-x}$  においては，横の長さxの値3に対しては縦の長さ7が唯一対応しyの値となる．横の長さxの値6に対しては4が唯一対応しyの値となる．右図参照．これらの関係を関数$f$を使って表すと

${\displaystyle f\left(3\right)=7}$ ， ${\displaystyle f\left(6\right)=4}$

となる．

長方形を作るには，xの値は

${\displaystyle 0<x<10}$

でなければならない．更に，xの値に対応するyの値は

${\displaystyle 0<y<10}$

となる．

一般に，関数${\displaystyle y=f\left(x\right)}$において，変数xの値のとりうる値の範囲，すなわちxの変域を，この関数の定義域という．また， xの定義域に対応する関数の値のとりうる範囲，すなわちyの変域を，この関数の値域という．

上記のひもで長方形を作る場合

定義域は${\displaystyle 0<x<10}$，値域は${\displaystyle 0<y<10}$

となる．

ホーム>>カテゴリー別分類>>関数>>関数

最終更新日： 2024年2月7日

[ページトップ]

利用規約

google translate (English version)