|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
応用分野:
三角関数の相互関係
, ベクトルを用いた三角関数の合成公式の導出
, 1・サイン・コサイン三角形を用いた三角関数の相互関係の導出
, 余弦定理
, 中線定理
, 2直線が垂直に交わる条件
, 2点間の距離
問題リスト←このページに関連している問題です
三平方の定理(ピタゴラスの定理)
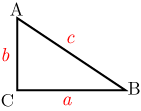 となる直角三角形
において,各辺の長さを,,
, とすると
となる直角三角形
において,各辺の長さを,,
, とすると
の関係が成り立つ.この関係を三平方の定理あるいはピタゴラスの定理という.
■証明
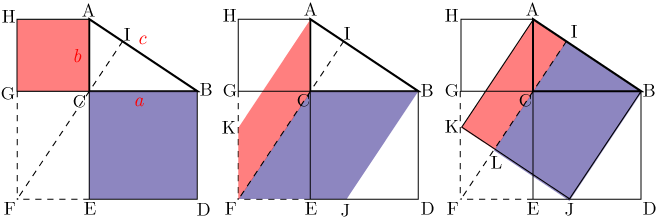
△ において,辺 を一辺と知る正方形 を描き,同じく辺 を一辺とする正方形 を下図の左側のように描く.直線 と直線 の交点を とし,直線 と直線 の交点を とする.
まず,直線 と直線 の関係を調べる.
四角形 は長方形で,,, となる.
よって
△ ≡△ (∵2辺とその間の角が等しい)
次に, について考える.
(∵対角は等しい), (△ ≡△ )より
よって
△ ∽△ (∵2角が等しい)
以上より
次に,面積が保たれる変形を繰り返すことにより,定理を証明する.
正方形の面積=平行四辺形 の面積 (∵ 共通で高さが同じ) ・・・・・・(1)
正方形 の面積=平行四辺形 の面積 (∵ 共通で高さが同じ) ・・・・・・(2)
さらに
平行四辺形 の面積=長方形 の面積 (∵ 共通で高さが同じ) ・・・・・・(3)
平行四辺形 の面積=長方形 の面積 (∵ 共通で高さが同じ) ・・・・・・(4)
(1),(2),(3),(4)より
四角形 の面積=正方形 の面積+正方形 の面積 ・・・・・・(5)
一方
, , より△ ≡△
よって
となり
四角形 は正方形 ・・・・・・(6)
となる.(5),(6)より
正方形 の面積=正方形 の面積+正方形 の面積
となる.すなわち
となる.
三平方の定理の証明は,この他にもいろいろな方法がる.
ホーム>>カテゴリー分類>>幾何>>三平方の定理(ピタゴラスの定理)
最終更新日: 2023年10月2日