関連するページを見るにはこのグラフ図を利用してください．

立体の重心

ある立体があり，その断面積が変数${\displaystyle x}$ の関数${\displaystyle S\left(x\right)}$として表せるとき，その区間${\displaystyle \left[a,b\right]}$ における立体の重心の ${\displaystyle x}$ 座標${\displaystyle x_G}$ は

${\displaystyle x_G=\frac{1}{V}{\displaystyle {\int }_a^{b}xS\left(x\right)dx}}$

■導出

体積の質量${\displaystyle M}$ を求める．

ある立体があり，その断面積が変数${\displaystyle x}$ の関数${\displaystyle S\left(x\right)}$として表せるとき，その区間${\displaystyle \left[a,b\right]}$ における立体の体積${\displaystyle V}$は

${\displaystyle V={\displaystyle {\int }_a^{b}S\left(x\right)}dx}$ ･････(1)（体積の計算を参照）

である．ここで，体積${\displaystyle V}$の密度（単位体積あたりの質量）を${\displaystyle \rho }$とすると，立体の全質量${\displaystyle M}$ は

${\displaystyle M=\rho V}$　･･････(2)

であり，(1)より

${\displaystyle M=\rho {\displaystyle {\int }_a^{b}S\left(x\right)}dx}$　･･････(3)

となる．

次に，立体の重心の${\displaystyle x}$座標${\displaystyle x_G}$を求める．

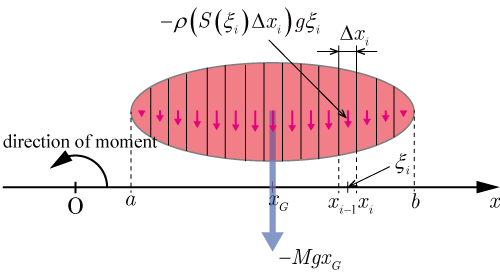「重心」の定義は「物体の各部分に働く重力の合力の作用点」であり，${\displaystyle x}$ 軸と交わり${\displaystyle x}$ 軸と重力の方向に垂直な回転軸の回りに関して「重力による力のモーメント」＝「各々の力のモーメントの和（連続体の場合は積分）」が成り立たつ．力のモーメントの正方向が反時計回りの方向であることを考慮すると

${\displaystyle -Mg{x}_G=-\underset{n\to \infty }{\lim }{\displaystyle \sum _{i=1}^n\rho \left(S\left({\xi }_i\right)\Delta x_i\right)g{\xi }_i}}$

(${\displaystyle g}$ は重力加速度の大きさ，${\displaystyle {\xi }_i}$ の位置の微小は厚さ${\displaystyle \Delta x_i}$ の薄板の質量は${\displaystyle \rho \left(S\left({\xi }_i\right)\Delta x_i\right)}$ ，重力は${\displaystyle \rho \left(S\left({\xi }_i\right)\Delta x_i\right)g}$ )

${\displaystyle -Mg{x}_G=-\rho g\underset{n\to \infty }{\lim }{\displaystyle \sum _{i=1}^n{\xi }_i\left(S\left({\xi }_i\right)\Delta x_i\right)}}$

定積分の定義より

${\displaystyle -Mg{x}_G=-\rho g{\displaystyle {\int }_a^{b}xS\left(x\right)dx}}$

${\displaystyle x_G=\frac{\rho }{M}{\displaystyle {\int }_a^{b}xS\left(x\right)dx}}$

(2)から

${\displaystyle =\frac{\rho }{\rho V}{\displaystyle {\int }_a^{b}xS\left(x\right)dx}}$

${\displaystyle =\frac{1}{V}{\displaystyle {\int }_a^{b}xS\left(x\right)dx}}$

(1)から

${\displaystyle =\frac{{\displaystyle {\int }_a^{b}xS\left(x\right)dx}}{{\displaystyle {\int }_a^{b}S\left(x\right)dx}}}$

　

■回転体の重心

立体の重心を利用することで，回転体の重心を求めることができる．

回転体の重心の求め方→ここ

 

ホーム>>カテゴリー分類>>積分 >>立体の重心の計算

学生スタッフ作成
最終更新日： 2023年11月24日

[ページトップ]

利用規約

google translate (English version)