log(
1+x
)
のマクローリン展開
log(
1+x
)=x−
1
2
x
2
+
1
3
x
3
−
1
4
x
4
+⋯
■導出
f(
x
)=log(
1+x
)
とおく．
f(
0
)=log1=0
f
'
(
x
)=
1
1+x
(
1+x
)
'
=
1
1+x
⋅1
=
(
1+x
)
−1
f
'
(
0
)=1
f
''
(
x
)=(
−1
)
(
1+x
)
−2
(
1+x
)
'
=(
−1
)
(
1+x
)
−2
⋅1
=−
(
1+x
)
−2
f
''
(
0
)=−1
f
'''
(
x
)=(
−2
)(
−1
)
(
1+x
)
−3
(
1+x
)
'
=2!
(
1+x
)
−3
f
'''
(
0
)=2!
f
(
4
)
(
x
)=(
−3
)(
2!
)
(
1+x
)
−4
(
1+x
)
'
=−3!
(
1+x
)
−4
f
(
4
)
(
0
)=−3!
f
5
x
=−
−4
3!
1+x
−5
1+x
'
=4!
1+x
−5
f
(
5
)
(
0
)=4!
したがって，マクローリン展開の公式
f(
x
)=f(
0
)+
f
'
(
0
)x+
f
''
(
0
)
2!
x
2
+
f
'''
(
0
)
3!
x
3
+⋯⋯
+
f
(
n
)
(
0
)
n!
x
n
+⋯⋯
に代入して
log
1+x
=0+1⋅x+
−1
2!
x
2
+
2!
3!
x
3
+
−3!
4!
x
4
+⋯
=x−
1
2
x
2
+
1
3
x
3
−
1
4
x
4
+⋯
■収束半径
a
n
=
(
−1
)
n−1
(
n−1
)!
n!
，
a
n+1
=
(
−1
)
n
n!
(
n+1
)!
lim
n→∞
|
a
n+1
a
n
|
=
lim
n→∞
|
(
−1
)
n
n!
(
n+1
)!
(
−1
)
n−1
(
n−1
)!
n!
|
=
lim
n→∞
|
(
−1
)
n
(
−1
)
n−1
⋅
n!
(
n+1
)!
⋅
n!
(
n−1
)!
|
=
lim
n→∞
|
−
n
n+1
|
=
lim
n→∞
|
−
1
1+
1
n
|
=1
よって，収束半径
R
は
R=
1
1
=1
となる．
x
の値が収束半径と等しいとき，
x−
1
2
x
2
+
1
3
x
3
−
1
4
x
4
+⋯⋯
の収束性について検討する．
x=1
のとき
1
1
−
1
2
+
1
3
−
1
4
+
1
5
−
1
6
+⋯⋯
=(
1
1
−
1
2
)+(
1
3
−
1
4
)+(
1
5
−
1
6
)+⋯⋯
=
2−1
1⋅2
+
4−3
3⋅4
+
6−5
5⋅6
+⋯⋯
=
1
1⋅2
+
1
3⋅4
+
1
5⋅6
+⋯⋯
=
lim
n→∞
∑
k=1
n
1
(
2k−1
)2k
<
lim
n→∞
∑
k=1
n
1
(
2k−1
)
2
(
∵
1
(
2k−1
)2k
<
1
(
2k−1
)
2
)
<1+
lim
n→∞
∫
1
n
1
(
2x−1
)
2
dx
=1+
lim
n→∞
[
−
1
2x−1
]
1
n
=1+
lim
n→∞
(
−
1
2n−1
+1
)
=2
となり，収束する．
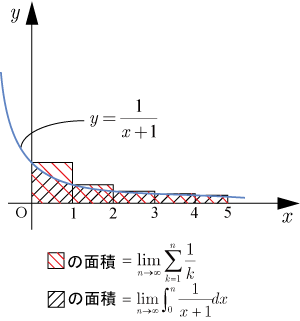
x
=
−
1
のとき
−
1
1
−
1
2
−
1
3
−−
1
4
−⋯⋯
=
lim
n→∞
∑
k=1
n
(
−
1
k
)
>
lim
n→∞
∫
0
n
(
−
1
x+1
)dx
=
lim
n→∞
[
−log(
x+1
)
]
0
n
=
lim
n→∞
[
−log(
n+1
)−log1
]
=
lim
n→∞
{
−log(
n+1
)
}
=−∞
となり，発散する．以上より，
x−
1
2
x
2
+
1
3
x
3
−
1
4
x
4
+⋯⋯
が収束する
x
の範囲は
−1<x≤1
となる．
ホーム>>カテゴリー分類>>数列>>級数展開>>マクローリン展開>>
log(
1+x
)
のマクローリン展開
最終更新日：
2022年7月19日
|
