|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
応用分野:
力のモーメント(トルク)
, 角運動量
, ベクトルのモーメント
, ベクトル積の表現行列
, 外積の大きさ
, 外積の成分表示
, 外積の計算則 交換
, 外積の計算則 結合
, 外積の計算則 分配
, 外積の計算則 結合法則は不成立
, 基本ベクトルにおける外積
,続きを見る
問題リスト←このページに関連している問題です
外積
■外積の定義
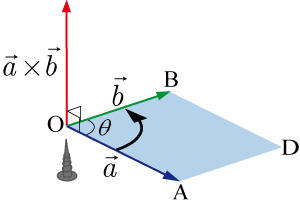 ,
の外積の定義を以下に示す(右図を参照のこと).
,
の外積の定義を以下に示す(右図を参照のこと).
- , の外積は と表わす.
- はベクトルである.
- ベクトルの大きさ
は
である.ただし, は と のなす角である.言い換えると,ベクトルの大きさ は と を2辺とする平行四辺形OADBの面積にとなる. - ベクトルの向きは, と に垂直で, と の始点を重ね を180°より小さい角度で に重ねるために始点を回転の中心として回転させる方向に右ネジを回した時に右ネジが進む方向である.
■外積の成分表示 ⇒
, のとき
■外積の基本的性質(計算則)
■基本ベクトルの外積 ⇒
■外積の計算の仕方 ⇒
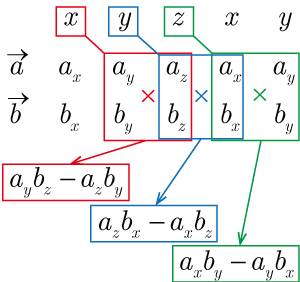
■行列式を用いた外積の計算 ⇒
, のとき
最終更新日 2025年4月27日