|
関連するページを見るにはこのグラフ図を利用してください.
問題リスト←このページに関連している問題です
単振動 (simple harmonic motion)
ある物理量 が,時刻 の関数として
- - - (1)
で与えられる運動をするとき,その運動を 単振動 (simple harmonic motion) という( , , は定数). を 振幅 (amplitude) といい, は の間を往復運動する.cos 関数の角度部分 を 位相 (phase) といい, は 初期位相 (initial phase)( のときの位相)である.単振動では, を 角振動数 (angular frequency)(または固有角振動数)とよぶ.多くの場合,物理量 は物体(質点)の位置を表し,単振動の代表的な例がばね‐質量系である.
単振動 について,横軸に時刻 ,縦軸に をとってグラフを描くと下図のようになる.
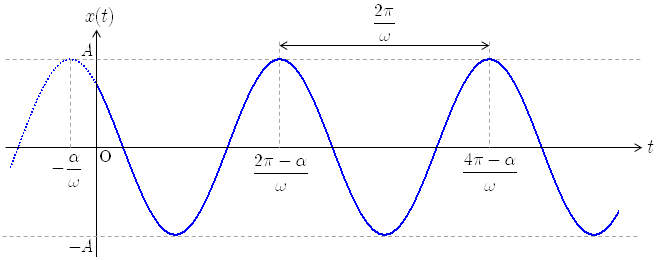
上述の単振動の表式は,三角関数の性質 を用いて,
- - - (2)
のように,sin 関数でも表せる.また,加法定理を用いて,
- - - (3)
,
のように,cos 関数とsin 関数の1次結合としても表せる.よって,これらの表式も単振動である.
単振動が現れる現象としては,ばね‐質量系の他に,単振り子,浮力による単振動,LC回路の電気振動などがある.