問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

曲線の長さを求める問題

■問題

曲線  ${\displaystyle y=\frac{1}{2}{x}^2}$ ${\displaystyle \left(0\leqq x\leqq 1\right)}$ の長さを求めよ．

■解説動画

◇積分の動画一覧のページへ

■答

${\displaystyle \frac{\sqrt{2}}{2}+\frac{1}{2}\log \left(1+\sqrt{2}\right)}$

ヒント

曲線の長さを参考にする

■解説

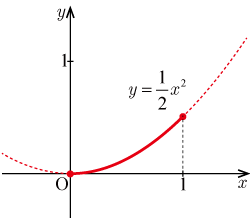
図の赤の実線部分の長さを求める．

${\displaystyle y=\frac{1}{2}{x}^2}$ ， ${\displaystyle y^{\prime }=x}$

よって，曲線の長さ $L$ は公式より

${\displaystyle L={\displaystyle {\int }_0^1\sqrt{1+x^2}dx}}$

となる． ${\displaystyle x=\tan t}$ とおく置換積分にによって値を求める．

${\displaystyle \frac{dx}{dt}=\frac{1}{{\cos }^{2}t}}$ →　 ${\displaystyle dx=\frac{1}{{\cos }^{2}t}dt}$

よって

${\displaystyle ={\displaystyle {\int }_0^{\frac{\pi }{4}}\sqrt{1+{\tan }^{2}t}}\cdot \frac{1}{{\cos }^{2}t}dt}$

${\displaystyle ={\displaystyle {\int }_0^{\frac{\pi }{4}}\sqrt{\frac{1}{{\cos }^{2}t}}}\cdot \frac{1}{{\cos }^{2}t}dt}$

${\displaystyle 0<t<\frac{\pi }{4}}$ では， ${\displaystyle \cos t>0}$ ．よって

${\displaystyle ={\displaystyle {\int }_0^{\frac{\pi }{4}}\frac{1}{\cos t}}\cdot \frac{1}{{\cos }^{2}t}dt}$

${\displaystyle ={\displaystyle {\int }_0^{\frac{\pi }{4}}\frac{1}{{\cos }^{3}t}dt}}$

${\displaystyle ={\displaystyle {\int }_0^{\frac{\pi }{4}}\frac{\cos t}{{\cos }^{4}t}}dt}$

${\displaystyle ={\displaystyle {\int }_0^{\frac{\pi }{4}}\frac{\cos t}{{(1-{\sin }^{2}t)}^2}}dt}$

${\displaystyle u=\sin t}$ とおく．

${\displaystyle \frac{du}{dt}=\cos t}$ →　 ${\displaystyle \cos tdt=du}$

よって

${\displaystyle ={\displaystyle {\int }_0^{\frac{1}{\sqrt{2}}}\frac{1}{{(1-u^2)}^2}}du}$

${\displaystyle ={\displaystyle {\int }_0^{\frac{1}{\sqrt{2}}}\frac{1}{{(1-u)}^2{(1+u)}^2}}du}$

ここで，被積分関数を部分分数に分解する．

・分子の計算

${\displaystyle a+b+2\left(a+b\right)u+\left(a+b\right)u^2}$ ${\displaystyle -bu-2b{u}^2-b{u}^3}$ ${\displaystyle c+d-2\left(c+d\right)u+\left(c+d\right)u^2}$ ${\displaystyle du-2d{u}^2+d{u}^3}$

${\displaystyle =a+b+c+d}$ ${\displaystyle +\left(2a+b-2c-d\right)t}$ ${\displaystyle +\left(a-b+c-d\right)t^2}$ ${\displaystyle +\left(-b+d\right)t^3}$

ここで

${\displaystyle a+b+c+d=1}$ ･･････(1)

${\displaystyle 2a+b-2c-d=0}$ ･･････(2)

${\displaystyle a-b+c-d=0}$ ･･････(3)

${\displaystyle -b+d=0}$ ･･････(4)

である．(4)より

${\displaystyle d=b}$ ･･････(5)

(5)を(2)に代入

${\displaystyle 2a+b-2c-b=0}$

${\displaystyle a-c=0}$

${\displaystyle a=c}$ ･･････(6)

(5)を(3)に代入

${\displaystyle a-b+c-b=0}$

${\displaystyle a+c-2b=0}$

これに(6)を代入

${\displaystyle a+a-2b=0}$

${\displaystyle 2a-2b=0}$

${\displaystyle a=b}$ ･･････(7)

(7)と(5)より

${\displaystyle d=a}$ ･･････(8)

(6)，(7)，(8)を(1)に代入

${\displaystyle a+a+a+a=1}$

${\displaystyle 4a=1}$

${\displaystyle a=\frac{1}{4}}$

よって

${\displaystyle a=b=c=d=\frac{1}{4}}$

となる．したがって

${\displaystyle ={\displaystyle {\int }_0^{\frac{1}{\sqrt{2}}}\frac{1}{{\left(1-u\right)}^2{\left(1+u\right)}^2}}}$

${\displaystyle =\frac{1}{4}\left\{2\sqrt{2}+\log \left(3+2\sqrt{2}\right)\right\}}$

${\displaystyle =\frac{\sqrt{2}}{2}+\frac{1}{4}\log \left(3+2\sqrt{2}\right)}$

${\displaystyle =\frac{\sqrt{2}}{2}+\frac{1}{4}\log {\left(\sqrt{2}+1\right)}^2}$

${\displaystyle =\frac{\sqrt{2}}{2}+\frac{1}{2}\log \left(\sqrt{2}+1\right)}$

 

■別解

${\displaystyle L={\displaystyle {\int }_0^1\sqrt{1+x^2}dx}}$

部分積分法を用いて計算をする．

${\displaystyle ={\displaystyle {\int }_0^1{\left(x\right)}^{\text{'}}\sqrt{1+x^2}dx}}$

${\displaystyle ={\left[x\sqrt{1+x^2}\right]}_0^1-{\displaystyle {\int }_0^{1}x\frac{1}{2}\frac{2x}{\sqrt{1+x^2}}}dx}$

${\displaystyle =\sqrt{2}-{\displaystyle {\int }_0^1\frac{x^2}{\sqrt{1+x^2}}dx}}$

${\displaystyle =\sqrt{2}-{\displaystyle {\int }_0^1\frac{1+x^2-1}{\sqrt{1+x^2}}dx}}$

${\displaystyle =\sqrt{2}-L+{\left[\log \left|x+\sqrt{1+x^2}\right|\right]}_0^1}$

${\displaystyle =\sqrt{2}-L+\log \left(1+\sqrt{2}\right)}$

よって

${\displaystyle 2L=\sqrt{2}+\log \left(1+\sqrt{2}\right)}$

${\displaystyle L=\frac{\sqrt{2}}{2}+\frac{1}{2}\log \left(1+\sqrt{2}\right)}$

 

ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>>曲線の長さ

学生スタッフ作成
最終更新日：2025年2月21日

[ページトップ]

利用規約

google translate (English version)