三角形の面積を求める問題
■問題
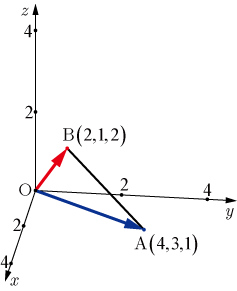
原点と空間上の2点
,
を頂点とする三角形の面積を求めよ.
■解説動画
■答
■ヒント
三角形の面積:
を用いる.この公式を覚えていない場合は,三角形の面積
×底辺の長さ×高さ,から計算をする.
外積の定義を参考にする.
■解説
●ベクトルの内積を用いた計算
三角形
の面積を
とすると
この式の内容は三角形の面積に詳しく書いてある
となる.
であることより
となる.よって
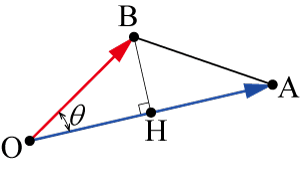
◇三角形の面積
×底辺の長さ×高さからの計算
★別解
とおくと
より
よって
以上より
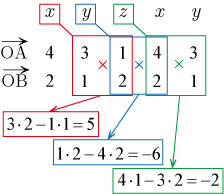
●ベクトルの外積を用いた計算
外積
の大きさ
は,
と
を2辺とする平行四辺形の面積になる(外積の定義を参照).よって,三角形
の面積
は
となる.
よって
となる.
■3Dグラフ
ホーム>>カテゴリー分類>>ベクトル>>ベクトルに関する問題>>三角形の面積を求める問題
最終更新日:
2025年10月20日 ->