関連するページを見るにはこのグラフ図を利用してください．

三角関数の定義

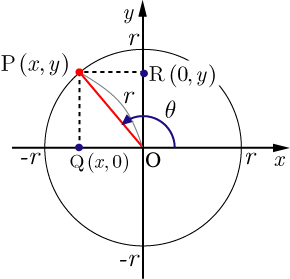原点を中心として半径 r  の円周上に点 $\text{P}$ ${\displaystyle \left(x,y\right)}$  があり， $x$ 軸の正方向と ${\displaystyle \text{OP}}$ のなす角を $\theta$ とする． 三角関数（正弦，余弦，正接，正割，余割，余接）は

正弦 せいげん （サイン）：  ${\displaystyle sin\theta =\frac{y}{r}}$

余弦 よげん （コサイン）：  ${\displaystyle cos\theta =\frac{x}{r}}$

正接 せいげん （タンジェント）：  ${\displaystyle tan\theta =\frac{y}{x}}$

正割 せいかつ （セカント）：  ${\displaystyle \sec \theta =\frac{1}{\cos \theta }=\frac{r}{x}}$

余割 よかつ （コセカント）：  ${\displaystyle \mathrm{cosec}\theta or\csc \theta =\frac{1}{\sin \theta }=\frac{r}{y}}$

余接 よせつ （コタンジェント）：  ${\displaystyle cot\theta =\frac{1}{\tan \theta }=\frac{x}{y}}$

と定義される．ただし

${\displaystyle r=\sqrt{x^2+y^2}}$

である．

また， ${\displaystyle x=0}$  のとき，すなわち， ${\displaystyle \theta =90°\pm 180°\times n}$  ( $n$  は整数) のとき ${\displaystyle tan\theta }$ ， $\sec \theta$ の値は存在しない． ${\displaystyle y=0}$  のとき，すなわち， ${\displaystyle \theta =\pm 180°\times n}$  ( $n$  は整数) のとき ${\displaystyle cot\theta }$ ， $\csc \theta$ の値は存在しない．

点 $\text{P}$ の座標を三角関数を用いて表すと

${\displaystyle \left(x,y\right)=\left(r\cos \theta ,r\sin \theta \right)}$

となる．

⇒三角比を参照のこと

特に，半径が1の場合の右下図の円のことを単位円といい，単位円を用いると

正弦（サイン）： ${\displaystyle sin\theta =y}$

余弦（コサイン）： ${\displaystyle cos\theta =x}$  

${\displaystyle \left(x,y\right)=\left(\cos \theta ,\sin \theta \right)}$

となり，点 $\text{P}$ の $y$ 座標が正接（sine）， $x$ 座標が余弦(cosine)となる．

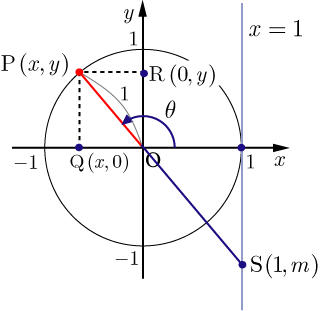また， $\text{OP}$ の延長線と ${\displaystyle x=1}$ との交点を $\text{S}$ とし，その $y$ 座標の値を $m$ とすると

正接（タンジェント）： ${\displaystyle tan\theta =m}$  

となる．⇒ 証明

単位円と各三角関数の関係も参照のこと

 

ホーム>>カテゴリー分類>>三角関数>>三角関数の定義

最終更新日： 2025年2月13日

[ページトップ]

利用規約

google translate (English version)