ベクトルに関する問題
ベクトルに関する動画一覧⇒こちらへ
解答の右上に*の印がついているものは,解説動画があることを示す.
- 基本問題
-
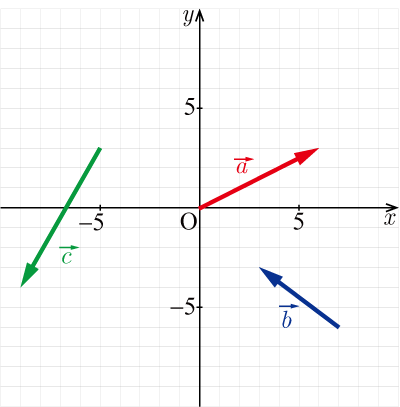
図の
,
,
を成分表示で表し,そのベクトル大きさを求めよ.⇒解答
-
,
のとき,
を求めよ.また,
を
と
を用いて表せ.⇒解答*
-
をベクトルの始点を中心として反時計回りに60°回転したベクトルを求めよ.⇒解答*
-
,
とする.
[1]
が
から
に変化したとき,
の終点の軌跡は直線を描く.どのような直線か答よ.
[2]
と
が平行な関係になるときの
の値を求めよ.
[3]
と
が垂直な関係になるときの
の値を求めよ
⇒解答*
- 点
と直線
の距離を求めよ.
は媒介変数である.⇒解答*
- △点
において,線分
を
に内分する点を点
,
を
に外分する点を点
,
を
に内分する点を点
とする.線分
と線分
の交点を点
とする.
,
とおくとき,
を
,
を用いて表せ.⇒解答
- 平面上のベクトル
- p平面ベクトル
,
の内積を求めよ. ⇒解答*
- 平面ベクトル
,
の内積を求めよ. ⇒解答
- 平面ベクトル
,
のなす角を求めよ. ⇒解答*
- 平面ベクトル
,
のなす角を求めよ. ⇒解答
-
,
とするとき,
と
が直交するような
を求めよ. ⇒解答*
-
,
とするとき,
と
が直交するような
を求めよ. ⇒解答
-
に垂直な単位ベクトルを求めよ. ⇒解答*
- 三角形
の頂点
,
,
の位置ベクトルを
,
,
とする.
この三角形
の重心
の位置を
,
,
を用いて表せ. ⇒解答
- 三角形
の各頂点
,
,
と各対辺の中点のを結ぶ3つの線分(中線)は1点で交わることを示せ. ⇒解答
- 三角形
の辺
の中点を
とすると
が成り立つ(中線定理)ことを,ベクトルを用いて証明せよ. ⇒解答
- 2つの直線
と
(
,
,
,
は定数)が直交するとき,
,
の間にどのような関係があるか,方向ベクトルを用いて求めよ. ⇒解答
- 空間におけるベクトル
- 空間ベクトル
,
の内積を求めよ. ⇒解答*
- 空間ベクトル
,
のなす角を求めよ. ⇒解答*
- 空間ベクトル
,
のなす角を
とするとき,
求めよ. ⇒解答
-
,
のベクトルの外積
を求めよ. ⇒解答*
-
,
,
の外積
を求めよ. ⇒解答
-
,
,
の外積
を求めよ. ⇒解答
-
,
,
の外積
を求めよ. ⇒解答*
-
,
,
の外積
を求めよ. ⇒解答*
- 原点と空間上の2点
,
を頂点とする三角形の面積を求めよ. ⇒解答*
- 空間上の3点
,
,
を頂点とする三角形の面積を求めよ. ⇒解答*
ホーム>>カテゴリー分類>>ベクトル>>ベクトルに関する問題
学生スタッフ
最終更新日:
2026年1月21日