演習問題
■単振り子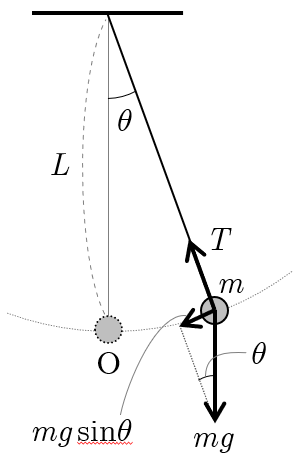
図のように,長さ L の伸縮しない軽い糸に質量 m の小球をつけて,振幅の小さな振動をさせる.重力加速度の大きさを g とすると,小球が鉛直線から角 θ だけずれたとき,小球に作用する力の軌道の接線方向成分は
F=−mgsinθ
である.このとき,原点Oからの小球の移動距離(弧の長さ)は s=Lθ であるので,小球の加速度の接線方向成分は
a=d2sdt2=d2(Lθ)dt2=Ld2θdt2
と表せる.以下の問に答えよ.
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■ラプラス変換に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■2階線形微分方程式に関する問題
■微分方程式の問題
■微分演算子,逆演算子に関する問題
■微分演算子,逆演算子に関する問題
次の微分方程式の一般解を求めなさい.
(D2−8D+15)y=e4x