平均値の定理
となる が少なくとも1つ存在する.
より
( , )
と置き換えると,平均値の定理は
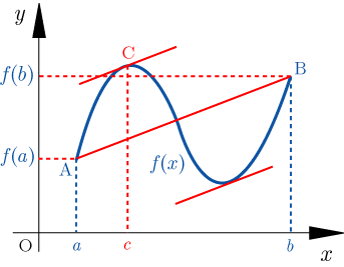
関数 が閉区間 で連続,開区間 で微分可能ならば,
となる が少なくとも1つ存在する
となる.
■証明
2点, を結ぶ線分をグラフとする関数 は
となる.
・・・・・(1)
とおく.
- 仮定より,関数 は閉区間 で連続,開区間 で微分可能である.
はi,ii,iiiよりロルの定理の条件を満たしている.よって
「 となるとなる が少なくとも1つ存在する.」 ・・・・・(2)
(1)より
・・・・・(3)
となり,(2)を(3)を使って書き換えると平均値の定理を得る.
【参考図書】
Calculus 7E 著者:James Stewart 出版社:Brooks/Cole Pub Co
最終更新日:2025年6月30日
 関数 が
関数 が