関連するページを見るにはこのグラフ図を利用してください．

重積分の定義

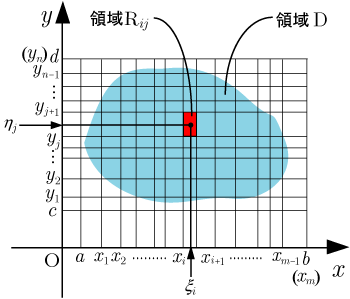2変数関数 ${\displaystyle z=f\left(x,y\right)}$ は境界を含む領域 ${\displaystyle D}$（水色の部分）で定義されている．

領域 ${\displaystyle D}$  は，長方形領域 ${\displaystyle R=\left\{\left(x,y\right)|a\leqq x\leqq b,c\leqq y\leqq d\right\}}$ に含まれるものとする．

${\displaystyle x}$ 成分の区間${\displaystyle \left[a,b\right]}$ を

${\displaystyle a=x_0<x_1<\cdots <x_{m-1}<x_m=b}$  

となる${\displaystyle x_i\left(i=0,1,2,\cdots ,m\right)}$ で${\displaystyle m}$個の小区間に分割し，${\displaystyle y}$ 成分の区間${\displaystyle \left[c,d\right]}$を

${\displaystyle c=y_0<y_1<\cdots <y_{n-1}<y_n=d}$  

となる${\displaystyle y_j\left(j=0,1,2,\cdots ,n\right)}$  で ${\displaystyle n}$個の小区間に分割する．

領域 ${\displaystyle R_{ij}}$  を

と定義し，${\displaystyle R_{ij}}$  の面積を${\displaystyle \Delta S_{ij}}$  とする．また${\displaystyle \left({\xi }_i,{\eta }_i\right)\in R_{ij}}$  とする．

領域 ${\displaystyle D}$ に含まれる ${\displaystyle R_{ij}}$ に関して

${\displaystyle f\left({\xi }_i,{\eta }_i\right)\Delta S_{ij}}$

を足し合わせた値

${\displaystyle V_{mn}={\displaystyle \sum _i{\displaystyle \sum _{j}f\left({\xi }_i,{\eta }_i\right)\Delta S_{ij}}}}$

を考える．

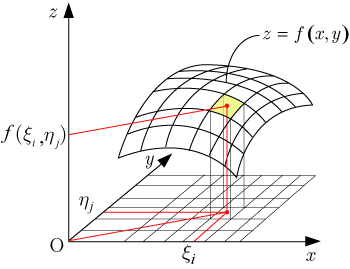
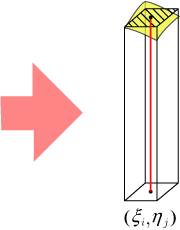
分割数${\displaystyle m,n}$ を大きくしていくと，分割の仕方および${\displaystyle {\xi }_i,{\eta }_i}$ のとり方に関係なくある値 ${\displaystyle V}$ に収束するなら，式で表すと

${\displaystyle V_{mn}=\underset{\begin{array}{l}m\to \infty \\ n\to \infty \end{array}}{\lim }{\displaystyle \sum _i{\displaystyle \sum _{j}f\left({\xi }_i,{\eta }_i\right)\Delta S_{ij}}}}$  

となるなら，${\displaystyle f\left(x,y\right)}$は領域 ${\displaystyle D}$ において積分可能であるといい

${\displaystyle V={\displaystyle {\iint }_{D}f\left(x,y\right)}dxdy}$  

と表す．

この極値 ${\displaystyle V}$ を${\displaystyle f\left(x,y\right)}$の${\displaystyle D}$ における2重積分という．

 

ホーム>>カテゴリー別分類>>積分>>重積分>>重積分の定義

学生スタッフ作成
最終更新日： 2023年8月1日

[ページトップ]

利用規約

google translate (English version)